
����Ŀ����ͼ��AΪij���ξ�������ѹ۾��㣬�οͿɴ�B�������³��ȵ���С�۾�ƽ̨DE�۾���Ȼ������E�����������³�����A��������ʱ��A��������������ֱ�ӵ���C������֪��AC��BC��C��DE��BC��AC=200.4�ף�BD=100�ף��Ϧ�=30�㣬�Ϧ�=70������AE�ij���ԼΪ________�ף����ο����ݣ�sin70��0.94��cos70���0.34��tan70���2.25����

 ����5��2���ϵ�д�
����5��2���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣���֪����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��AB�ֱ���x��y�ύ�ڵ�B��A���뷴����������ͼ��ֱ��ڵ�C��D��CE��x���ڵ�E��tan��ABO=![]() ��OB=4��OE=2��
��OB=4��OE=2��
��1���ֱ�����÷�����������ֱ��AB�Ľ���ʽ��
��2���������D���꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ������������ÿ�����Ϊ40Ԫ��ƻ������۲��Ź涨ÿ���ۼ۲��ø���55Ԫ���г����鷢�֣���ÿ����50Ԫ�ļ۸����ۣ�ƽ��ÿ������90�䣬�۸�ÿ���1Ԫ��ƽ��ÿ��������3�䣮
��1����ƽ��ÿ��������![]() �������ۼ�
�������ۼ�![]() Ԫ/��֮��ĺ�����ϵʽ��
Ԫ/��֮��ĺ�����ϵʽ��
��2����ÿ��ƻ�������ۼ�![]() Ϊ����Ԫʱ������ʹ��õ���������w�����������Ƕ��٣�
Ϊ����Ԫʱ������ʹ��õ���������w�����������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������εĻ�̳���ָ��7�����֣������ı���PRBA��RQDC��QPFEΪ�����Ρ���������PRBA��RQDC��QPFE������ֱ�Ϊ![]() ��
��![]() ��
��![]() �� RH��PQ������ΪH��
�� RH��PQ������ΪH��
��1����PR��QR��![]() =16��
=16��![]() =9����
=9����![]() = ��RH= ��
= ��RH= ��
��2�����ı���PRBA��RQDC��QPFE������ֱ�Ϊ25m2��13m2��36m2

�����PRQ�������
�����жϡ�PRQ�͡�DEQ�������������ϵ����֤����Ľ��ۣ�
�������λ�̳ABCDEF���������������m2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����һԪ���η���x2=��1û��ʵ��������������һ��ʵ����ƽ�����ک�1�������ǹ涨һ������i��ʹ������i2=��1����x2=��1������һ����Ϊi�������ҽ�һ���涨��һ��ʵ�����������������������㣬��ԭ�е����㷨����Ȼ������������i1=i��i2=��1��i3=i2i=����1��i��i4=��i2��2=����1��2=1���Ӷ�������������n�����ǿɵõ�i4n+1=i4ni=��i4��ni��ͬ���ɵ�i4n+2=��1��i4n+3=��i��i4n=1����ô��i+i2+i3+i4+��+i2016+i2017��ֵΪ�� ��
A. 0 B. 1 C. ��1 D. i
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ⷽ��![]() �����˴����������£�
�����˴����������£�
�������߶�����![]() ����
����![]() �� ����һ����
�� ����һ����
ȥ���ţ��� ![]() �� ���ڶ�����
�� ���ڶ�����
����ϲ�ͬ����� ![]() �� ����������
�� ����������
��� ![]() �� �����IJ���
�� �����IJ���
�����飬![]() ��ԭ���̵Ľ⣮ �����岽��
��ԭ���̵Ľ⣮ �����岽��
��1��С���������Ǵӵ� ����ʼ�����ģ�ԭ���̻�Ϊ��һ���ĸ����� ��
��2����д��������ȷ�Ľ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
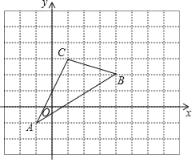
����Ŀ����ͼ��������ABC��ֱ������ϵ�У�
��1����ֱ��д����A��C��������꣺
��2��������ABC��������� ����
��3������������ABC����ƽ��1����λ��������ƽ��1����λ��������A��B��C����ͼ�л���������A��B��C������ʱ��B��������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�� ![]() ��ֱ������ƽ���ڣ��������������ֱ�Ϊ
��ֱ������ƽ���ڣ��������������ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��������������ÿ��С�����α߳���
��������������ÿ��С�����α߳���![]() ����λ���ȣ�
����λ���ȣ�
��![]() ��
��![]() ��
��![]() �Ƶ�__________��ʱ����ת__________�ȵõ��ģ�
�Ƶ�__________��ʱ����ת__________�ȵõ��ģ� ![]() ��������__________��
��������__________��
��![]() ������߶�
������߶�![]() ��ת��������ɨ����������������
��ת��������ɨ����������������![]() ����
����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڵȱߡ�ABC�У���P��Q��BC���ϵ��������㣨�����B��C�غϣ�����AP��AQ��
��1����ͼ1����֪����BAP��20�㣬���AQB�Ķ�����
��2����Q����ֱ��AC�ĶԳƵ�ΪM���ֱ�����AM��PM��
�ٵ���P�ֱ��ڵ�Q�����Ҳ�ʱ���������⽫ͼ2��ͼ3��ȫ����д��������
��С����������IJ��룺��P��Q���˶��Ĺ����У�ʼ����PA��PM������С����֤�������������ȷ�ģ������ڢٵĵ�P��Q������λ�ù�ϵ��ѡ��һ��˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com