
【题目】一个六边形的花坛被分割成7个部分,其中四边形PRBA,RQDC,QPFE为正方形。记正方形PRBA,RQDC,QPFE的面积分别为![]() ,
,![]() ,
,![]() , RH⊥PQ,垂足为H。
, RH⊥PQ,垂足为H。
(1)若PR⊥QR,![]() =16,
=16,![]() =9,则
=9,则![]() = ,RH= ;
= ,RH= ;
(2)若四边形PRBA,RQDC,QPFE的面积分别为25m2、13m2、36m2

①求△PRQ的面积;
②请判断△PRQ和△DEQ的面积的数量关系,并证明你的结论;
③六边形花坛ABCDEF的面积是 m2.
【答案】(1)25,2.4;(2)①9,②S△PRQ=S△DQE,证明见解析,③110.
【解析】
(1)由s1=16,s2=9,可知PR=4,RQ=3,利用勾股定理求出PQ=5,即可得解;
(2)①方法一:设PH=a,则QH=6-a,在Rt△PRH和Rt△QRH中分别利用勾股定理表示RH2,列出方程即可求出a,再利用勾股定理求出RH,即可求出△PRQ的面积;
方法二:设RH=h,利用勾股定理得出PH=![]() =
=![]() ,QH=
,QH=![]() =
=![]() ,根据PQ=6得到
,根据PQ=6得到![]() =6﹣
=6﹣![]() ,两边平方可求出h,即可得解;
,两边平方可求出h,即可得解;
②延长RQ到点M,使QM=RQ,连结PM,易证△DQE≌△MQP,得到S△DQE=S△MQP,由RQ=QM等底同高的三角形面积相等可知S△PRQ=S△MQP,等量代换得出S△PRQ=S△DQE;
③由①②可知,S△PRQ=S△DQE=S△BCR=S△APF,即可得解.
解:(1)∵s1=16,s2=9,
∴PR=4,RQ=3,
∵PR⊥QR,
∴PQ=![]() =5,
=5,
∴s3=25,RH=![]() =2.4;
=2.4;
(2)①方法一:设PH=a,则QH=6-a,
∵![]() ,
,
∴![]() ,
,
解得:a=4,
∴![]() =25-16=9,
=25-16=9,
∴RH=3,
∴S△PQR=![]() ×6×3=9;
×6×3=9;
方法二:如图,RH⊥PQ于H,设RH=h,

在Rt△PRH中,PH=![]() =
=![]() ,
,
在Rt△RQH中,QH=![]() =
=![]() ,
,
∴PQ=![]() +
+![]() =6,
=6,
![]() =6﹣
=6﹣![]() ,
,
两边平方得,25﹣h2=36﹣12![]() +13﹣h2,
+13﹣h2,
整理得,![]() =2,
=2,
两边平方得,13-h2=4,
解得h=3,
∴S△PQR=![]() ×6×3=9;
×6×3=9;
②S△PRQ=S△DQE,
证明:延长RQ到点M,使QM=RQ,连结PM,

∵QD=QM,∠DQE=∠MQP,QE=QP,
∴△DQE≌△MQP,
∴S△DQE=S△MQP,
∵RQ=QM,
∴S△PRQ=S△MQP,
∴S△PRQ=S△DQE;
③由②可知S△PRQ=S△DQE,同理S△PRQ=S△APF,
∵RB=RP,∠BRC=∠PRQ,RC=RQ,
∴△BRC≌△PRQ,
∴S△BRC=S△PRQ,
∵S△PQR=9,
∴六边形花坛ABCDEF的面积=25+13+36+4×9=74+36=110m2.
故答案为:(1)25,2.4;(2)①9,②S△PRQ=S△DQE,证明见解析,③110.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E,F分别在BC,AB上,点M在BA的延长线上,且CE=BF=AM,过点M,E分别作NM⊥DM,NE⊥DE交于N,连接NF.
(1)求证:DE⊥DM;
(2)猜想并写出四边形CENF是怎样的特殊四边形,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为:A(1,﹣4),B(5,﹣4),C(4,﹣1).
(1)将△ABC经过平移得到△A1B1C1,若点C的应点C1的坐标为(2,5),则点A,B的对应点A1,B1的坐标分别为 ;
(2)在如图的坐标系中画出△A1B1C1,并画出与△A1B1C1关于原点O成中心对称的△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】航拍无人机甲从海拔![]() 处出发,以
处出发,以![]() 匀速铅直上升,与此同时,航拍无人机乙从海拔
匀速铅直上升,与此同时,航拍无人机乙从海拔![]() 处出发,以
处出发,以![]() 匀速铅直上升.设无人机上升时间为
匀速铅直上升.设无人机上升时间为![]() ,无人机甲、乙所在位置的高度分别为
,无人机甲、乙所在位置的高度分别为![]() 、
、![]()
(1)根据题意,填写下表:
上升时间 | 5 | 10 |
|
| 25 |
| |
| 60 |
|
(2)请你分别写出![]() 、
、![]() 与
与![]() 的关系式;
的关系式;
(3)在某时刻两架无人机能否位于同一高度?若能,求无人机上升的时间和所在高度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学兴趣小组的同学调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图。依据图中信息,解答下列问题:

(1)接受这次调查的家长共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“很赞同”的家长占被调查家长总数的百分比是 ;
(4)在扇形统计图中,“不赞同”的家长部分所对应扇形的圆心角度数是 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩进行统计,并按照成绩从低到高分成A,B,C,D,E五个小组,绘制统计图如下(未完成),解答下列问题:
(1)样本容量为 ,频数分布直方图中a= ;
(2)扇形统计图中D小组所对应的扇形圆心角为n°,求n的值并补全频数分布直方图;
(3)若成绩在80分以上(不含80分)为优秀,全校共有2000名学生,估计成绩优秀的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,AC=200.4米,BD=100米,∠α=30°,∠β=70°,则AE的长度约为________米.(参考数据:sin70≈0.94,cos70°≈0.34,tan70°≈2.25).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司准备与汽车租凭公司签订租车合同,以每月用车路程xkm计算,甲汽车租凭公司每月收取的租赁费为y1元,乙汽车租凭公司每月收取的租赁费为y2元,若y1、y2与x之间的函数关系如图3所示,其中x=0对应的函数值为月固定租赁费,则下列判断错误的是( )
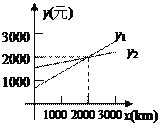
A. 当月用车路程为2000km时,两家汽车租赁公司租赁费用相同
B. 当月用车路程为2300km时,租赁乙汽车租赁公车比较合算
C. 除去月固定租赁费,甲租赁公司每公里收取的费用比乙租赁公司多
D. 甲租赁公司平均每公里收到的费用比乙租赁公司少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com