
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊжБЯпPQЁЮMNЃЌЕуAдкжБЯпPQЩЯЃЌЕуCЁЂDдкжБЯпMNЩЯЃЌСЌНгACЁЂADЃЌЁЯPACЃН50ЁуЃЌЁЯADCЃН30ЁуЃЌAEЦНЗжЁЯPADЃЌCEЦНЗжЁЯACDЃЌAEгыCEЯрНЛгкEЃЎ
ЃЈ1ЃЉЧѓЁЯAECЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєНЋЭМ1жаЕФЯпЖЮADбиMNЯђгвЦНвЦЕНA1D1ШчЭМ2ЫљЪОЮЛжУЃЌДЫЪБA1EЦНЗжЁЯAA1D1ЃЌCEЦНЗжЁЯACD1ЃЌA1EгыCEЯрНЛгкEЃЌЁЯPACЃН50ЁуЃЌЁЯA1D1CЃН30ЁуЃЌЧѓЁЯA1ECЕФЖШЪ§ЃЎ
ЃЈ3ЃЉШєНЋЭМ1жаЕФЯпЖЮADбиMNЯђзѓЦНвЦЕНA1D1ШчЭМ3ЫљЪОЮЛжУЃЌЦфЫћЬѕМўгыЃЈ2ЃЉЯрЭЌЃЌЧѓДЫЪБЁЯA1ECЕФЖШЪ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉЁЯAECЃН130ЁуЃЛЃЈ2ЃЉЁЯA1ECЃН130ЁуЃЛЃЈ3ЃЉЁЯA1ECЃН40ЁуЃЎ
ЁОНтЮіЁП
(1)гЩжБЯпPQЁЮMNЃЌЁЯADC=ЁЯQAD=30ЁуЃЌПЩЕУЁЯPAD=150ЁуЃЌдйЧѓЁЯPAE=75ЁуЃЌПЩЕУЁЯCAE=25ЁуЃЛгЩЁЯPAC=ЁЯACNЃЌЧѓЕУЁЯECA=25ЁуЃЌЙЪЁЯAEC=180ЁуЉ25ЁуЉ25ЁуЃЛ
(2)ЯШЧѓГіЁЯQA1D1=30ЁуЃЌЁЯPA1D1=150ЁуЃЌдйЧѓГіЁЯPA1E=ЁЯEA1D1=75ЁуЃЌдйЧѓГіЁЯCAQ=130ЁуЃЌЁЯACN=50ЁуЃЌИљОнЦНЗжЯпЖЈвхЕУЁЯACE=25ЁуЃЌдйРћгУЫФБпаЮФкНЧКЭаджЪПЩЧѓЁЯCEA1ЃЛ
(3)ИљОнЦНааЯпаджЪКЭНЧЦНЗжЯпЖЈвхПЩЧѓЕУЁЯQA1E=ЁЯ2=15ЁуЃЌЁЯACE=ЁЯECN=ЁЯ1=25ЁуЃЌдйгЩЁЯCEA1=ЁЯ1+ЁЯ2МДПЩЧѓЕУД№АИ.
(1)ШчЭМ1ЫљЪОЃК

ЁпжБЯпPQЁЮMNЃЌЁЯADCЃН30ЁуЃЌ
ЁрЁЯADCЃНЁЯQADЃН30ЁуЃЌ
ЁрЁЯPADЃН150ЁуЃЌ
ЁпЁЯPACЃН50ЁуЃЌAEЦНЗжЁЯPADЃЌ
ЁрЁЯPAEЃН75ЁуЃЌ
ЁрЁЯCAEЃН25ЁуЃЌ
ПЩЕУЁЯPACЃНЁЯACNЃН50ЁуЃЌ
ЁпCEЦНЗжЁЯACDЃЌ
ЁрЁЯECAЃН25ЁуЃЌ
ЁрЁЯAECЃН180ЁуЉ25ЁуЉ25ЁуЃН130ЁуЃЛ
(2)ШчЭМ2ЫљЪОЃК
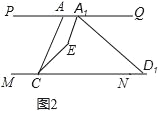
ЁпЁЯA1D1CЃН30ЁуЃЌЯпЖЮADбиMNЯђгвЦНвЦЕНA1D1ЃЌPQЁЮMNЃЌ
ЁрЁЯQA1D1ЃН30ЁуЃЌ
ЁрЁЯPA1D1ЃН150ЁуЃЌ
ЁпA1EЦНЗжЁЯAA1D1ЃЌ
ЁрЁЯPA1EЃНЁЯEA1D1ЃН75ЁуЃЌ
ЁпЁЯPACЃН50ЁуЃЌPQЁЮMNЃЌ
ЁрЁЯCAQЃН130ЁуЃЌЁЯACNЃН50ЁуЃЌ
ЁпCEЦНЗжЁЯACD1ЃЌ
ЁрЁЯACEЃН25ЁуЃЌ
ЁрЁЯCEA1ЃН360ЁуЉ25ЁуЉ130ЁуЉ75ЁуЃН130ЁуЃЛ
(3)ШчЭМ3ЫљЪОЃК
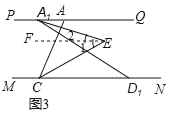
Й§ЕуEзїFEЁЮPQЃЌ
ЁпЁЯA1D1CЃН30ЁуЃЌЯпЖЮADбиMNЯђзѓЦНвЦЕНA1D1ЃЌPQЁЮMNЃЌ
ЁрЁЯQA1D1ЃН30ЁуЃЌ
ЁпA1EЦНЗжЁЯAA1D1ЃЌ
ЁрЁЯQA1EЃНЁЯ2ЃН15ЁуЃЌ
ЁпЁЯPACЃН50ЁуЃЌPQЁЮMNЃЌ
ЁрЁЯACNЃН50ЁуЃЌ
ЁпCEЦНЗжЁЯACD1ЃЌ
ЁрЁЯACEЃНЁЯECNЃНЁЯ1ЃН25ЁуЃЌ
ЁрЁЯCEA1ЃНЁЯ1+ЁЯ2ЃН15Ёу+25ЁуЃН40ЁуЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЃЌжБЯпl3КЭжБЯпl1ЃЌl2НЛгкCЁЂDСНЕуЃЌЕуPдкжБЯпCDЩЯЃЎ
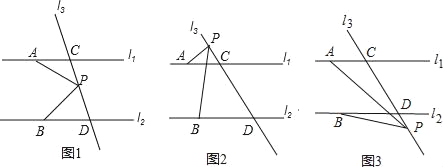
(1)ЪдаДГіЭМ1жаЁЯAPBЁЂЁЯPACЁЂЁЯPBDжЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
(2)ШчЙћPЕудкCЁЂDжЎМфдЫЖЏЪБЃЌЁЯAPBЁЂЁЯPACЁЂЁЯPBDжЎМфЕФЙиЯЕЛсЗЂЩњБфЛЏТ№ЃП
Д№ЃКЁЁ ЁЁ(ЬюЗЂЩњЛђВЛЗЂЩњ)
(3)ШєЕуPдкCЁЂDСНЕуЕФЭтВрдЫЖЏЪБ(PЕугыЕуCЁЂDВЛжиКЯ)ЃЌШчЭМ2ЃЌЭМ3ЃЌЪдЗжeаДГіЁЯPACЁЂЁЯAPBЁЂЁЯPBDжЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
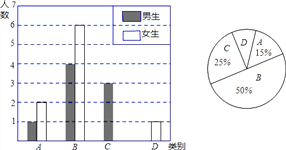
ЁОЬтФПЁПЮвЯиЪЕЪЉаТПЮГЬИФИяКѓЃЌбЇЩњЕФзджїбЇЯАЁЂКЯзїНЛСїФмСІгаКмДѓЬсИпЃЌКњРЯЪІЮЊСЫСЫНтАрМЖбЇЩњзджїбЇЯАЁЂКЯзїНЛСїЕФОпЬхЧщПіЃЌЖдФГАрВПЗжбЇЩњНјааСЫЮЊЦкАыИідТЕФИњзйЕїВщЃЌВЂНЋЕїВщНсЙћЗжГЩЫФРрЃЌAЃКЬиБ№КУЃЛBЃККУЃЛCЃКвЛАуЃЛDЃКНЯВюЃЛВЂНЋЕїВщНсЙћЛцжЦГЩвдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЕїВщжаЃЌКњРЯЪІвЛЙВЕїВщСЫЁЁ УћЭЌбЇЃЌЦфжаХЎЩњЙВгаЁЁ ___УћЃЛ
ЃЈ2ЃЉНЋЩЯУцЕФЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉЮЊСЫЙВЭЌНјВНЃЌКњРЯЪІЯыДгБЛЕїВщЕФAРрКЭDРрбЇЩњжаЗжБ№бЁШЁвЛЮЛЭЌбЇНјааЁАвЛАявЛЁБЛЅжњбЇЯАЃЌЧыгУСаБэЗЈЛђЛЪїаЮЭМЕФЗНЗЈЧѓГіЫљбЁСНЮЛЭЌбЇЧЁКУЪЧвЛЮЛФаЭЌбЇКЭвЛЮЛХЎЭЌбЇЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЩфЛїЖгЮЊДгМзЁЂввСНУћдЫЖЏдБжабЁАЮвЛШЫВЮМгЪЁБШШќЃЌЖдЫћУЧНјааСЫСљДЮВтЪдЃЌВтЪдГЩМЈШчЯТБэ![]() ЕЅЮЛЃКЛЗ
ЕЅЮЛЃКЛЗ![]() ЃК
ЃК
Ек1ДЮ | Ек2ДЮ | Ек3ДЮ | Ек4ДЮ | Ек5ДЮ | Ек6ДЮ | |
Мз | 10 | 9 | 8 | 8 | 10 | 9 |
вв | 10 | 10 | 8 | 10 | 7 | 9 |
ИљОнБэИёжаЕФЪ§ОнЃЌПЩМЦЫуГіМзЁЂввСНШЫЕФЦНОљГЩМЈЖМЪЧ9ЛЗЃЎ
ЃЈ1ЃЉЗжБ№МЦЫуМзЁЂввСљДЮВтЪдГЩМЈЕФЗНВюЃЛ
ЃЈ2ЃЉИљОнЪ§ОнЗжЮіЕФжЊЪЖЃЌФуШЯЮЊбЁ______УћЖгдБВЮШќЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ1ИіЕЅЮЛГЄЖШЕФаЁе§ЗНаЮзщГЩЕФЭјИёжаЃЌИјГіСЫИёЕуЁїABCЃЈЖЅЕуЪЧЭјИёЯпЕФНЛЕуЃЉКЭИёЕуPЃЎ
ЃЈ1ЃЉвдAЕуЮЊЮЛЫЦжааФЃЌНЋЁїABCдкЭјИёжаЗХДѓГЩЁїAB1C1ЃЌЪЙ![]() =2ЃЌЧыЛГіЁїAB1C1ЃЛ
=2ЃЌЧыЛГіЁїAB1C1ЃЛ
ЃЈ2ЃЉвдPЕуЮЊШ§НЧаЮЕФвЛИіЖЅЕуЃЌЧыЛвЛИіИёЕуЁїPMNЃЌЪЙЁїPMNЁзЁїABCЃЌЧвЯрЫЦБШЮЊ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпl3ЃЌl4гыl1ЃЌl2ЗжБ№ЯрНЛгкЕуAЁЂBЁЂCЁЂDЃЌЧвЁЯ1+ЁЯ2ЃН180ЁуЃЎ
ЃЈ1ЃЉжБЯпl1гыl2ЦНааТ№ЃПЮЊЪВУДЃП
ЃЈ2ЃЉЕуEдкЯпЖЮADЩЯЃЌЁЯABEЃН30ЁуЃЌЁЯBECЃН62ЁуЃЌЧѓЁЯDCEЕФЖШЪ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌжБЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() гы
гы![]() Йигк
Йигк![]() жсЖдГЦЃЌНЛ
жсЖдГЦЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌ
ЃЌ
ЃЈ1ЃЉЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙ§Еу![]() дк
дк![]() ЭтзїжБЯп
ЭтзїжБЯп![]() ЃЌЙ§
ЃЌЙ§![]() Еузї
Еузї![]() гкЕу
гкЕу![]() ,Й§
,Й§![]() Еузї
Еузї![]() гкЕу
гкЕу ![]() ЃЎЧѓжЄЃК
ЃЎЧѓжЄЃК![]()
ЃЈ3ЃЉШчЭМ2ЃЌШчЙћ![]() би
би![]() жсЯђгвЦНвЦЃЌ
жсЯђгвЦНвЦЃЌ![]() БпНЛ
БпНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() ЕФбгГЄЯпЩЯЕФвЛЕуЃЌЧв
ЕФбгГЄЯпЩЯЕФвЛЕуЃЌЧв![]() ЃЌ
ЃЌ![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌдк
ЃЌдк![]() ЦНвЦЕФЙ§ГЬжаЃЌ
ЦНвЦЕФЙ§ГЬжаЃЌ![]() ЕФГЄЖШЪЧЗёЮЊЖЈжЕЃЌЧыЫЕУїРэгЩЃЎ
ЕФГЄЖШЪЧЗёЮЊЖЈжЕЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЫљЪОЃЌБпГЄЮЊaЕФе§ЗНаЮжагавЛИіБпГЄЮЊbЕФаЁе§ЗНаЮЃЌШчЭМ2ЫљЪОЪЧгЩЭМ1жавѕгАВПЗжЦДГЩЕФвЛИіе§ЗНаЮЃЎ
ЃЈ1ЃЉЩшЭМ1жавѕгАВПЗжУцЛ§ЮЊS1ЃЌЭМ2жавѕгАВПЗжУцЛ§ЮЊS2ЃЎЧыжБНггУКЌaЃЌbЕФДњЪ§ЪНБэЪОS1ЃЌS2ЃЛ
ЃЈ2ЃЉЧыаДГіЩЯЪіЙ§ГЬЫљНвЪОЕФГЫЗЈЙЋЪНЃЛ
ЃЈ3ЃЉЪдРћгУетИіЙЋЪНМЦЫуЃКЃЈ2+1ЃЉЃЈ22+1ЃЉЃЈ24+1ЃЉЃЈ28+1ЃЉ+1ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
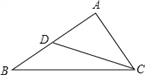
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЁїABCжаЃЌDЪЧABЕФжаЕуЃЌЧвЁЯACD=ЁЯBЃЌШє AB=10ЃЌЧѓACЕФГЄЃЎ
ЁОД№АИЁП5![]() .
.
ЁОНтЮіЁПЪдЬтЗжЮіЃК
гЩЕуDЪЧABЕФжаЕуЃЌAB=10ЃЌвзЕУAD=5ЃЛдйгЩЁЯACD=ЁЯBЃЌЁЯA=ЁЯAЃЌПЩжЄЕУЃК
ЁїACDЁзЁїABCЃЌДгЖјПЩЕУЃК ![]() ЃЌгЩДЫЕУЕНЃКAC2=AD
ЃЌгЩДЫЕУЕНЃКAC2=AD![]() AB=50МДПЩНтЕУACЕФжЕ.
AB=50МДПЩНтЕУACЕФжЕ.
ЪдЬтНтЮіЃК
ЁпЁЯACD=ЁЯBЃЌЁЯA=ЁЯAЃЌ
ЁрЁїACDЁзЁїABCЃЎ
Ёр![]() ЃЌ
ЃЌ
ЁрAC2=AD![]() AB.
AB.
ЁпDЪЧABЕФжаЕуЃЌAB=10ЃЌ
ЁрAD=![]() AB=5,
AB=5,
ЁрAC2=50ЃЎ
НтЕУAC=![]() .
.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
22
ЁОЬтФПЁППкДќжазАгаЫФИіДѓаЁЭъШЋЯрЭЌЕФаЁЧђЃЌАбЫќУЧЗжБ№БъКХ1,2,3,4ЃЌДгжаЫцЛњУўГівЛИіЧђЃЌМЧЯТЪ§зжКѓЗХЛиЃЌдйДгжаЫцЛњУўГівЛИіЧђЃЌРћгУЪїзДЭМЛђепБэИёЧѓГіСНДЮУўЕНЕФаЁЧђЪ§КЭЕШгк4ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com