

���� ��1����ͼ1�У���ֱ��BM������AD��MD������֤��OE=$\frac{1}{2}$DM����֤��AC=DM���ɣ�
��2������֤��OD=OB����tan��ODC=$\frac{1}{2}$=$\frac{OE}{OD}$����OE=a��OD=2a����EB=OE=a��BD=2a$\sqrt{2}$��t��an��EBH=tan��ODE=$\frac{1}{2}$=$\frac{HE}{HB}$���Ƴ�EH=$\frac{\sqrt{5}}{5}$a��HB=$\frac{2\sqrt{5}}{5}$a����Rt��DHB�У�����DH=$\sqrt{B{D}^{2}-B{H}^{2}}$�����DH���ɽ�����⣮
��3����ͼ3�У�����DF��BC����BM��GD��M������֤����FDG�ա�BDC���Ƴ�BC=FG=2���Ƴ�BH=CH=$\sqrt{2}$��DH=BM=3$\sqrt{2}$���ɡ�CFB=��CDB���Ƴ�tan��CFB=tan��CDB=$\frac{1}{3}$=$\frac{BC}{CF}$���Ƴ�CF=6��CG=CF+GF=8���Ƴ�DG=CD=4$\sqrt{2}$��BG=$\sqrt{C{G}^{2}+B{C}^{2}}$=2$\sqrt{17}$����$\frac{1}{2}$•BG•DP=$\frac{1}{2}$•DG•BM�����DP���ٸ��ݹ��ɶ������PG���ɡ�GPK�ס�GCB��$\frac{GK}{BG}$=$\frac{PG}{CG}$�����GK���ɽ�����⣮
��� ��1��֤������ͼ1�У���ֱ��BM������AD��MD��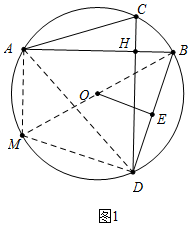
��OE��BD��
��BE=ED����OB=OM��
��OE=$\frac{1}{2}$DM��
��BM��ֱ����AB��CD��
���MAB=��DHB=90�㣬
��AM��CD��
���MAD=��ADC��
��$\widehat{DM}$=$\widehat{AC}$��
��DM=AC��
��OE=$\frac{1}{2}$AC��
��2����ͼ2�У�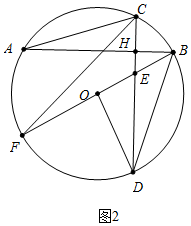
�ߡ�FCD=45�㣬
���DOF=2��FCD=90�㣬��DBF=��DCF=45�㣬
���ODB=��OBD=45�㣬
��OD=OB��
��tan��ODC=$\frac{1}{2}$=$\frac{OE}{OD}$����OE=a��OD=2a����EB=OE=a��BD=2a$\sqrt{2}$��
�ߡ�EOD=��EHB=90�㣬��OED=��BEH��
���ODE=��EBH��
��tan��EBH=tan��ODE=$\frac{1}{2}$=$\frac{HE}{HB}$��
��EH=$\frac{\sqrt{5}}{5}$a��HB=$\frac{2\sqrt{5}}{5}$a��
��Rt��DHB��DH=$\sqrt{B{D}^{2}-B{H}^{2}}$=$\sqrt{��2a\sqrt{2}��^{2}-��\frac{2\sqrt{5}}{5}a��^{2}}$=$\frac{6\sqrt{5}}{5}$a��
�ߡ�A=��CDB��
��tan��A=tan��CDB=$\frac{HB}{HD}$=$\frac{\frac{2\sqrt{5}}{5}a}{\frac{6\sqrt{5}}{5}a}$=$\frac{1}{3}$��
��3����ͼ3�У�����DF��BC����BM��GD��M��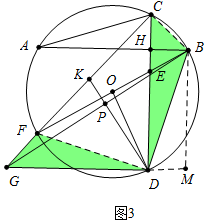
�ߡ�GCD=��FBD=45�㣬��CDG=��BDF=90�㣬
���CDG����BDF�ǵ���ֱ�������Σ�
��DF=DB��DG=DC����FDG=��BDC��
���FDG�ա�BDC��
��BC=FG=2��
��BH=CH=$\sqrt{2}$��DH=BM=3$\sqrt{2}$��
�ߡ�CFB=��CDB��
��tan��CFB=tan��CDB=$\frac{1}{3}$=$\frac{BC}{CF}$��
��CF=6��CG=CF+GF=8��
��DG=CD=4$\sqrt{2}$��BG=$\sqrt{C{G}^{2}+B{C}^{2}}$=2$\sqrt{17}$��
��DP��BG��
��$\frac{1}{2}$•BG•DP=$\frac{1}{2}$•DG•BM��
��DP=$\frac{4\sqrt{2}��3\sqrt{2}}{2\sqrt{17}}$=$\frac{12}{\sqrt{17}}$��
��PG=$\sqrt{G{D}^{2}-D{P}^{2}}$=$\frac{20}{\sqrt{17}}$��
�ɡ�GPK�ס�GCB��$\frac{GK}{BG}$=$\frac{PG}{CG}$��
��$\frac{GK}{2\sqrt{17}}$=$\frac{\frac{20}{\sqrt{17}}}{8}$��
��GK=5��
��KF=GK-FG=5-2=3��
���� ���⿼��Բ�ۺ��⡢ȫ�������ε��ж������ʡ����������ε��ж������ʡ��������������ɶ�����֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ӳ��ø����߹���ȫ�������ν�����⣬�����п�ѹ���⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
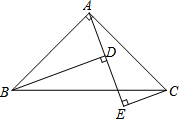 ��ͼ����֪��ABC�У���BAC=90�㣬AB=AC��B��C��A��E����࣬BD��AE��D��CE��AE��E��
��ͼ����֪��ABC�У���BAC=90�㣬AB=AC��B��C��A��E����࣬BD��AE��D��CE��AE��E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | -$\frac{1}{2}$ | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com