
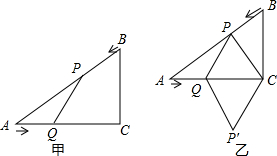
 ��ͼ�ף��ڡ�ABC�У���ACB=90�㣬AC=4cm��BC=3cm�������P�ɵ�B������BA�������A�����˶���ͬʱ��Q�ɵ�A������AC�������C�����˶������ǵ��ٶȾ�Ϊ1cm/s������PQ�����˶�ʱ��Ϊt��s����0��t��4��������������⣺
��ͼ�ף��ڡ�ABC�У���ACB=90�㣬AC=4cm��BC=3cm�������P�ɵ�B������BA�������A�����˶���ͬʱ��Q�ɵ�A������AC�������C�����˶������ǵ��ٶȾ�Ϊ1cm/s������PQ�����˶�ʱ��Ϊt��s����0��t��4��������������⣺| PH |
| BC |
| AP |
| AB |
| PH |
| 3 |
| 5-t |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| AE |
| AC |
| AP |
| AB |
| 4 |
| 5 |
| 1 |
| 2 |
| 9 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| 9 |
| 5 |
|
|
|
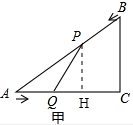 �⣺��1����ͼ�ף�����P��PH��AC��H��
�⣺��1����ͼ�ף�����P��PH��AC��H��| PH |
| BC |
| AP |
| AB |
| PH |
| 3 |
| 5-t |
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
| 5 |
| 2 |
| 15 |
| 8 |
| 5 |
| 2 |
| 15 |
| 8 |
| AE |
| AC |
| AP |
| AB |
| AP•AC |
| AB |
| (5-t)��4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 9 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 5 |
| 1 |
| 2 |
| 20 |
| 13 |
| 20 |
| 13 |
| 20 |
| 13 |
| 3 |
| 5 |
| 9 |
| 5 |
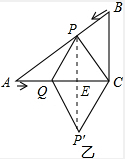
| PE2+QE2 |
(-
|
|
| 5 |
| 2 |
|
| 25 |
| 13 |
|
| 40 |
| 13 |
| 5 |
| 2 |
| 25 |
| 13 |
| 40 |
| 13 |


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
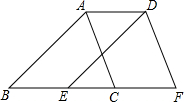 ��ͼ����B��E��C��F��ͬһֱ���ϣ�AB=DE����B=��DEF��BE=CF��
��ͼ����B��E��C��F��ͬһֱ���ϣ�AB=DE����B=��DEF��BE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 һ���쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ������������ʻ����ʻ��ʱ��Ϊx��ʱ��������֮��ľ���Ϊy��ǧ�ף���ͼ�е����߱�ʾ�������������쳵�����ҵع�����y��x֮��ĺ�����ϵ��
һ���쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ������������ʻ����ʻ��ʱ��Ϊx��ʱ��������֮��ľ���Ϊy��ǧ�ף���ͼ�е����߱�ʾ�������������쳵�����ҵع�����y��x֮��ĺ�����ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��֪����ͼ���ı���ABCDΪƽ���ı��Σ���CDΪֱ������O����O���BC�ཻ�ڵ�F����O������DE���AB�ཻ�ڵ�E����AE=3EB��
��֪����ͼ���ı���ABCDΪƽ���ı��Σ���CDΪֱ������O����O���BC�ཻ�ڵ�F����O������DE���AB�ཻ�ڵ�E����AE=3EB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
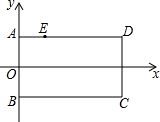 ��ͼ����֪����ABCD��AB��y���ϣ�AB=2��BC=3����A������Ϊ��0��1������AD������һ��E��1��1��������E��ֱ��ƽ�־���ABCD����������ֱ�ߵĽ���ʽΪ
��ͼ����֪����ABCD��AB��y���ϣ�AB=2��BC=3����A������Ϊ��0��1������AD������һ��E��1��1��������E��ֱ��ƽ�־���ABCD����������ֱ�ߵĽ���ʽΪ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��һ������Ӫ��У�С��ͬѧ��Ӫ��A������Ҫ��A�صı�ƫ�� 60�㷽���C����������������������200m����B�أ����ر�ƫ��30�㷽���ߣ�ǡ�ܵ���Ŀ�ĵ�C����ͼ������ô���ɴ˿�֪��B��C�������
��һ������Ӫ��У�С��ͬѧ��Ӫ��A������Ҫ��A�صı�ƫ�� 60�㷽���C����������������������200m����B�أ����ر�ƫ��30�㷽���ߣ�ǡ�ܵ���Ŀ�ĵ�C����ͼ������ô���ɴ˿�֪��B��C��������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com