

| A.25°或50° | B.20°或50° | C.40°或50° | D.40°或80° |
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源:不详 题型:解答题
 中,点
中,点 是线段
是线段 上一动点,
上一动点, 为
为 的中点,
的中点, 的延长线交
的延长线交 于
于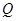 .
.
 ;(4分)
;(4分) ,
, 从点
从点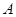 出发,以1cm/s的速度向
出发,以1cm/s的速度向 运动(不与
运动(不与 重合).设点
重合).设点 运动时间为
运动时间为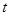 秒,请用
秒,请用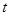 表示
表示 的长;并求
的长;并求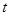 为何值时,四边形
为何值时,四边形 是菱形.(6分)
是菱形.(6分)查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.2cm | B.3cm | C.2.5cm | D. cm cm |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为 ;③EB⊥ED;④S△APD+S△APB=
;③EB⊥ED;④S△APD+S△APB= .其中正确结论的序号是
.其中正确结论的序号是
| A.①③④ | B.①②③ | C.②③④ | D.①②④ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com