
【题目】如图,PB为⊙O的切线,B为切点,过B作OP的垂线BA,垂足为C,交⊙O于点A,连接PA,AO,并延长AO交⊙O于点E,与PB的延长线交于点D.

(1) 求证:PA是⊙O的切线;
(2) 若![]() ,且OC=4,求PA的长.
,且OC=4,求PA的长.
【答案】(1)证明见解析;(2)3![]() .
.
【解析】
试题分析: (1)连接OB,先由等腰三角形的三线合一的性质可得:OP是线段AB的垂直平分线,进而可得:PA=PB,然后证明△PAO≌△PBO,进而可得∠PBO=∠PAO,然后根据切线的性质可得∠PBO=90°,进而可得:∠PAO=90°,进而可证:PA是⊙O的切线;
(2)连接BE,由![]() ,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.
,且OC=4,可求AC,OA的值,然后根据射影定理可求PC的值,从而可求OP的值,然后根据勾股定理可求AP的值.
试题解析:(1)连接OB,则OA=OB,

∵OP⊥AB,
∴AC=BC,
∴OP是AB的垂直平分线,
∴PA=PB,
在△PAO和△PBO中,
∵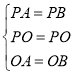 ,
,
∴△PAO≌△PBO(SSS)
∴∠PBO=∠PAO,PB=PA,
∵PB为⊙O的切线,B为切点,
∴∠PBO=90°,
∴∠PAO=90°,
即PA⊥OA,
∴PA是⊙O的切线;
(2)连接BE,
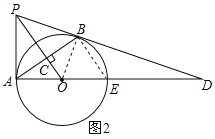
∵![]() ,且OC=4,
,且OC=4,
∴AC=6,
∴AB=12,
在Rt△ACO中,
由勾股定理得:AO=![]() ,
,
∴AE=2OA=4![]() ,OB=OA=2
,OB=OA=2![]() ,
,
在Rt△APO中,
∵AC⊥OP,
∴AC2=OC![]() PC,
PC,
解得:PC=9,
∴OP=PC+OC=13,
在Rt△APO中,由勾股定理得:AP=![]() =3
=3![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商店以每套80元的进价购进8套服装,并以90元左右的价格卖出.如果以90元为标准,超过标准的售价记为正数,不足标准的售价记为负数,出售价格记录如下:+2,﹣3,+5,+1,﹣2,﹣1,0,﹣5(单位:元).其它收支不计,当商店卖完这8套服装后( )
A. 盈利 B. 亏损 C. 不盈不亏 D. 盈亏不明
查看答案和解析>>
科目:初中数学 来源: 题型:
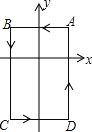
【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A—B—C-D—A一B一…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com