
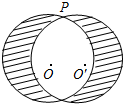
 如图,点P是⊙O上一点,⊙O的半径为4cm,以点P 为旋转中心,把⊙O逆时针旋转30°得到⊙O′,则图中阴影部分的面积是($\frac{16}{3}$π+16)cm2.(结果保留π)
如图,点P是⊙O上一点,⊙O的半径为4cm,以点P 为旋转中心,把⊙O逆时针旋转30°得到⊙O′,则图中阴影部分的面积是($\frac{16}{3}$π+16)cm2.(结果保留π) 分析 根据旋转的性质结合菱形的面积求法得出空白面积,进而利用:2(圆的面积-空白面积)=阴影部分的面积求出即可.
解答 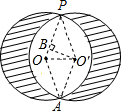 解:如图所示:连接PO,AO,AO′,PO′,过点O′作O′B⊥OP于点B,
解:如图所示:连接PO,AO,AO′,PO′,过点O′作O′B⊥OP于点B,
∵以点P 为旋转中心,把⊙O逆时针旋转30°得到⊙O′,
∴∠OPO′=30°,则∠PO′O=75°,故∠PO′A=150°,
故BO′=$\frac{1}{2}$PO′=2cm,
可得四边形POAO′是菱形,其面积为:PO×O′B=2×4=8(cm2),
故空白面积为:$\frac{150π×{4}^{2}}{360}$-8+$\frac{150π×{4}^{2}}{360}$=($\frac{40}{3}$π-8)cm2,
则图中阴影部分的面积是:2[π×42-($\frac{40}{3}$π-8)]=($\frac{16}{3}$π+16)cm2.
故答案为:($\frac{16}{3}$π+16).
点评 此题主要考查了扇形面积求法以及菱形面积求法等知识,根据题意求出空白面积是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
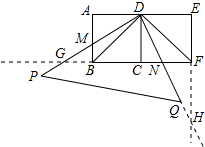 如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板(即Rt△PDQ)的直角顶点放置在点D处,DP交AB于点M,DQ交BF于点N.
如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板(即Rt△PDQ)的直角顶点放置在点D处,DP交AB于点M,DQ交BF于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
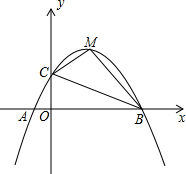 如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(-1,0),B(5,0)两点,与y轴交于点C(0,2)
如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(-1,0),B(5,0)两点,与y轴交于点C(0,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com