
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 设△ABC的面积为S,所求的第三条高线的长为h,则三边长分别为$\frac{2s}{5}$,$\frac{2s}{8}$,$\frac{2s}{h}$,然后根据三角形的三边关系列出不等式组求解即可.
解答 解:设△ABC的面积为S,所求的第三条高线的长为h,则三边长分别为$\frac{2s}{5}$,$\frac{2s}{8}$,$\frac{2s}{h}$,则$\frac{2s}{5}$>$\frac{2s}{8}$.
由三边关系,得 $\left\{\begin{array}{l}{\frac{2s}{8}+\frac{2s}{h}>\frac{2s}{5}}\\{\frac{2s}{8}+\frac{2s}{5}>\frac{2s}{h}}\end{array}\right.$,
解得$\frac{40}{13}$<h<$\frac{40}{3}$.
所以h的最小整数值为4,即第三条高线的长的最小值为4.
故选C.
点评 本题考查了三角形的边角关系,属于对三角形三边关系以及三角形基本知识的理解和运用,解题的关键是根据题意列出不等式组求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小华画出了一次函数y=-3x-3的图象的一部分,根据图象解答下面的问题:
如图,小华画出了一次函数y=-3x-3的图象的一部分,根据图象解答下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
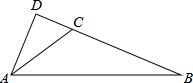 如图,在△ABC中,∠ACB=120°,AC=4,BC=6,过点A作BC的垂线,交BC的延长线于点D,则tanB的值为$\frac{\sqrt{3}}{4}$.
如图,在△ABC中,∠ACB=120°,AC=4,BC=6,过点A作BC的垂线,交BC的延长线于点D,则tanB的值为$\frac{\sqrt{3}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
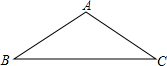 在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.
在等腰三角形中,过其中的一个顶点的直线如果能把这个等腰三角形分成两个小的等腰三角形,我们称这种等腰三角形为“少见的三角形”,这条直线称为分割线,下面我们来研究这类三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com