
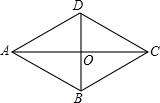
 如图,已知菱形ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,则AB=5.
如图,已知菱形ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,则AB=5.  春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当电流为定值时,电压y与电阻x | |
| B. | 某销售员计划一个月(30天)销售空调y台,每天销售x台 | |
| C. | 三角形的面积为定值G,一边长为x,这边上的高为y | |
| D. | 汽车在高速公路上匀速行驶,行驶路程y和行驶时间x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
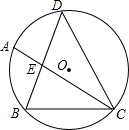 如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.
如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com