
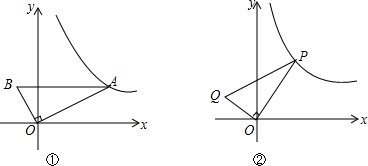
分析 (1)设AB与y轴交于点C,如图所示,根据OA=2OB,设OB=x,则有OA=2x,在直角三角形ABO中,利用勾股定理求出x的值,确定出OA与OB的长,利用面积法求出OC的长,在直角三角形AOC中,利用勾股定理求出AC的长,确定出A的坐标,代入反比例解析式求出k的值即可;
(2)分别过P,Q作PN⊥x轴,QM⊥x轴,利用同角的余角相等得到一对角相等,再由一对直角相等,得到三角形QOM与三角形PON相似,由相似得比例表示出PN与ON,进而表示出P坐标,代入反比例解析式即可确定出n与m的函数解析式;
(3)根据(2)的结论及题意确定出P与Q坐标,确定出QM,OM,PN,ON的长,三角形POQ面积=梯形PQMN面积-三角形QOM面积-三角形PNO面积,求出即可.
解答 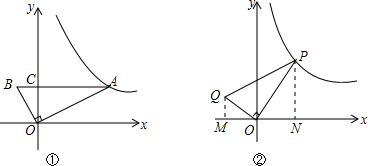 解:(1)设AB与y轴交于点C,如图所示,
解:(1)设AB与y轴交于点C,如图所示,
在Rt△AOB中,OA=2OB=2x,OB=x,AB=5,
根据勾股定理得:x2+(2x)2=52,
解得:x=$\sqrt{5}$,
∴OA=2$\sqrt{5}$,OB=$\sqrt{5}$,
∵S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OC,
∴OC=$\frac{OA•OB}{AB}$=$\frac{2\sqrt{5}×\sqrt{5}}{5}$=2,
在Rt△AOC中,根据勾股定理得:AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=4,
∴A(4,2),
把A坐标代入反比例解析式得:k=8;
故答案为:8;
(2)分别过P,Q作PN⊥x轴,QM⊥x轴,
∵∠QOM+∠OQM=90°,∠QOM+∠PON=90°,
∴∠OQM=∠PON,
∵∠QMO=∠PNO=90°,
∴△OQM∽△PON,
∴$\frac{QM}{ON}$=$\frac{OM}{PN}$=$\frac{OQ}{OP}$=$\frac{1}{2}$,
∵Q(m,n),
∴OM=-m,QM=n,
∴PN=-2m,ON=2n,即P(2n,-2m),
把P坐标代入反比例解析式得:-4mn=8,即-mn=2,
则n与m的函数解析式为n=-$\frac{2}{m}$(-2<m<-$\frac{1}{2}$);
(3)根据题意及(2)得:n=1,m=-2,即Q(-2,1),P(2,4),
∴QM=1,PN=4,OM=2,ON=2,即MN-2+2=4,
∴S△POQ=S梯形PQMN-S△QOM-S△PON=$\frac{1}{2}$×4×(1+4)-$\frac{1}{2}$×1×2-$\frac{1}{2}$×2×4=10-1-4=5.
点评 此题属于反比例函数综合题,涉及的知识有:坐标与图形性质,相似三角形的判定与性质,待定系数法确定反比例函数解析式,勾股定理,以及梯形,三角形面积求法,熟练掌握相似三角形的判定与性质是解本题第二问的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
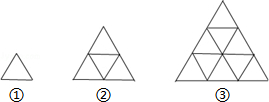
| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
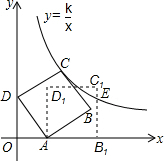 如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为5的正方形ABCD斜靠在y轴上,顶点A(3,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,得正方形AB1C1D1,且B1恰好落在x轴的正半轴上,此时边B1C1交反比例图象于点E,则点E的纵坐标是( )| A. | $\frac{5}{2}$ | B. | 3 | C. | $\frac{7}{2}$ | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com