
分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与使得一次函数y=kx+b的图象与两坐标轴围成的三角形面积不大于2的情况,再利用概率公式求解即可求得答案.
解答 解:画树状图得: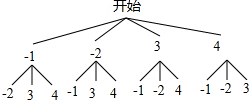
y=kx+b与两坐标轴的交点坐标为(-$\frac{b}{k}$,0)和(0,b),
∵一次函数y=kx+b的图象与两坐标轴围成的三角形面积不大于2,
∴$\frac{1}{2}$|-$\frac{b}{k}$|•|b|≤2,
即b2≥4k,或b2≤-4k,
由树状图知共有12种情况,满足b2≥4k,或b2≤-4k的有(-1,-2),(-2,-1),(3,-1),(3,-2),(4,-1),(4,-2),(4,3)7种情况,
∴P(一次函数y=kx+b的图象与两坐标轴围成的三角形面积不大于2)=$\frac{7}{12}$.
故答案为:$\frac{7}{12}$.
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;注意概率=所求情况数与总情况数之比.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
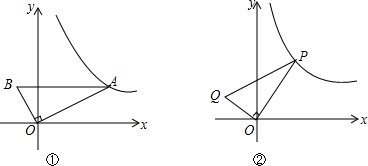
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
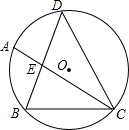 如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.
如图,△DBC内接于⊙O,DB=DC,$\widehat{AB}$=$\widehat{BC}$,DB交AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
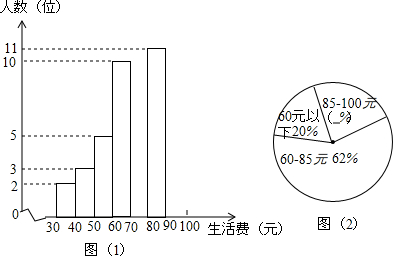
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.
阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com