
分析 (1)先把各二次根式化为最简二次根式即可;
(2)利用完全平方公式和平方差公式计算;
(3)分别解两个方程得到x≥-1和x<2,再确定不等式组的解集,然后在此解集内找出整数即可;
(4)先去分母,把分式方程化为整式方程,解整式方程得到x=-1,然后进行检验确定原方程的解.
解答 解:(1)原式=3$\sqrt{3}$-$\sqrt{x}$+$\frac{2\sqrt{6x}}{3}$;
(2)原式=5-6$\sqrt{5}$+9+11-9
=16-6$\sqrt{5}$;
(3)$\left\{\begin{array}{l}{5+2x≥3①}\\{\frac{x+1}{3}>\frac{1}{2}x②}\end{array}\right.$,
解①得x≥-1,
解②得x<2,
所以不等式组的解集为-1≤x<2,
所以不等式组的整数解为-1,0,1;
(3)去分母得2x=x-2+1,
解得x=-1,
经检验x=-1是原方程的解.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.也考查了解分式方程和一元一次不等式组.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
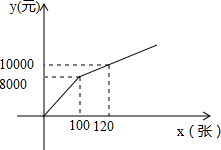 为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)
为丰富群众的业余生活,我市准备组织篮球比赛,市体育局策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).方案一:若单位赞助广告费8000元,则该单位所购门票的价格为每张50元;(总费用=广告赞助费+门票费)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
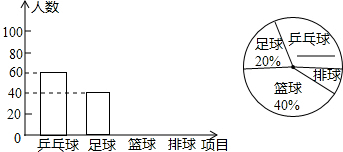
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
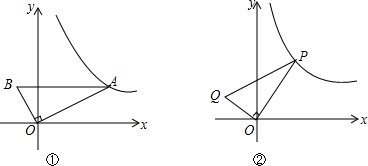
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com