
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
分析 首先根据题意列出表格,然后由表格即可求得所有等可能的结果与点P落在已知抛物线y=-4x+4上的情况,再利用概率公式即可求得答案.
解答 解:列表得:
| x y | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| 2 | (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| 3 | (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| 4 | (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| 5 | (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| 6 | (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:填空题
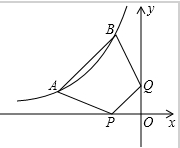 如图,A(a,1),B(-1,b)都在双曲线y=-$\frac{3}{x}$(x>0)点P,Q分别是x轴,y轴上的动点,当四边形PABQ的周长最小值时,PQ所在直线的解析式是y=x+2.
如图,A(a,1),B(-1,b)都在双曲线y=-$\frac{3}{x}$(x>0)点P,Q分别是x轴,y轴上的动点,当四边形PABQ的周长最小值时,PQ所在直线的解析式是y=x+2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<1 | B. | a≤1 | C. | a>1 | D. | a≥1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
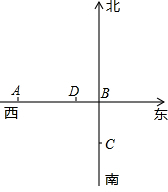 如图,从西到东的轻轨线经过A镇和B镇,两镇相距18千米,某公司C位于B镇的正南4千米处,现要从A镇把货物运往公司C,需要在轻轨线上的D处修筑通往公司C的公路.如果要使A镇到D处(沿轻轨)再到公司C处(沿公路)的总路程为20千米,那么D处距离A镇多少千米?
如图,从西到东的轻轨线经过A镇和B镇,两镇相距18千米,某公司C位于B镇的正南4千米处,现要从A镇把货物运往公司C,需要在轻轨线上的D处修筑通往公司C的公路.如果要使A镇到D处(沿轻轨)再到公司C处(沿公路)的总路程为20千米,那么D处距离A镇多少千米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com