
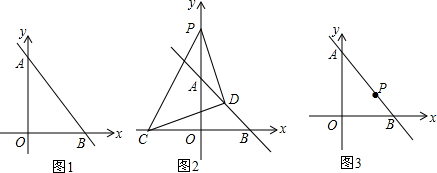
分析 (1)根据分式无意义可知a-4=0,从而可求得a=4,故此可求得OA=OB=4,最后利用三角形的面积公式求解即可;
(2)先根据点D为AB的中点可求得点D的坐标,然后求得CD的解析式,根据相互垂直的两条直线的一次项系数的乘积为-1,从而可求得DP的解析式,故此可求得点P的坐标;
(3)过点P作PD⊥AO,垂足为D,PC⊥OB,垂足为C,由平行线分线段成比例定理可求得m=2.8,n=1.2,然后代入所求的代数式可求得代数式的值.
解答 解:(1)∵分式$\frac{3}{a-4}$无意义,
∴a-4=0.
解得:a=4.
∴点A、B的坐标分别为(0,4),(4,0).
∴OA=OB=4.
∴S△AOB=$\frac{1}{2}OA•OB$=$\frac{1}{2}×4×4$=8.
(2)∵点A、B的坐标分别为(0,4),(4,0),点D为线段AB的中点,
∴点D的坐标为(2,2).
设CD的解析式为y=kx+b,
将点C和点D的坐标代入得:$\left\{\begin{array}{l}{-3k+b=0}\\{2k+b=2}\end{array}\right.$,
解得:k=$\frac{2}{5}$,b=$\frac{6}{5}$.
∴直线CD的解析式为y=$\frac{2}{5}x+\frac{6}{5}$.
∵△CDP为直角三角形,
∴直线PD的解析式的一次项系数为$-\frac{5}{2}$.
设直线DP的解析式为y=-$\frac{5}{2}x+c$,将点D的坐标代入得:$-\frac{5}{2}×2+c=2$,
解得:c=7.
∴直线DP的解析式为y=-$\frac{5}{2}x+7$.
将x=0代入得:y=7.
∴点P的坐标为(0,7).
(3)如图所示:过点P作PD⊥AO,垂足为D,PC⊥OB,垂足为C.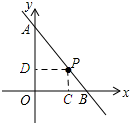
∵DP⊥OA,BO⊥OA,
∴DP∥OB,
∴$\frac{DP}{OB}=\frac{AP}{AB}=\frac{7}{10}$,即$\frac{DP}{4}=\frac{7}{10}$.
解得;DP=2.8.
∴m=2.8.
∵PC⊥OB,OA⊥OB,
∴PC∥OA.
∴$\frac{PC}{AO}=\frac{PB}{AB}=\frac{3}{10}$,即$\frac{n}{4}=\frac{3}{10}$.
解得:n=1.2.
∴$\frac{{m}^{2}{+n}^{2}}{2mn}$=$\frac{2.{8}^{2}+1.{2}^{2}}{2×2.8×1.2}$=$\frac{29}{21}$.
点评 本题主要考查的是一次函数的综合应用,解答本题需要同学熟练掌握一次函数的图象和性质、平行线分线段成比例定理,明确相互垂直的两直线的一次项系数的乘积是-1解题的关键.


科目:初中数学 来源: 题型:解答题
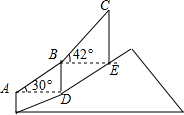 如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).
如图,登山缆车从点A出发,途径点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
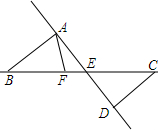 如图,直线AD,BC相交于点E,AB∥CD,F是直线BC上一点(F点与B,E,C三点不重合).
如图,直线AD,BC相交于点E,AB∥CD,F是直线BC上一点(F点与B,E,C三点不重合).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
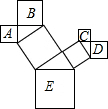 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、4、2、3,则最大正方形E的面积是38.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
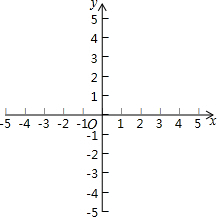 我们已经知道y=ax2+c的图象可以由函数y=ax2通过上、下平侈所得,例如,函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2的图象通过向下平移2个单位长度而得到,那么函数y=$\frac{1}{2}$(x-2)2的图象是否可由函数y=$\frac{1}{2}$x2的图象平移而得到呢?请在图中试一试,你能从中发现什么规律吗?
我们已经知道y=ax2+c的图象可以由函数y=ax2通过上、下平侈所得,例如,函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2的图象通过向下平移2个单位长度而得到,那么函数y=$\frac{1}{2}$(x-2)2的图象是否可由函数y=$\frac{1}{2}$x2的图象平移而得到呢?请在图中试一试,你能从中发现什么规律吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
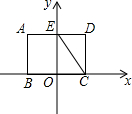 以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.
以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com