
分析 首先根据解答例题可得$\frac{{x}^{2}-x+1}{x}$=7,进而可得x+$\frac{1}{x}$=8,再求$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$的倒数的值,进而可得答案.
解答 解:∵$\frac{x}{{x}^{2}-x+1}$=$\frac{1}{7}$,
∴$\frac{{x}^{2}-x+1}{x}$=7,
x+$\frac{1}{x}$=8,
∵$\frac{{x}^{4}+{x}^{2}+1}{{x}^{2}}$=x2+$\frac{1}{{x}^{2}}$+1=(x+$\frac{1}{x}$)2-2+1=82-1=63,
∴$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$=$\frac{1}{63}$.
点评 此题主要考查了分式的混合运算,关键是理解例题的解法,掌握解题方法后,再根据例题方法解答.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 RT△ABC中,∠ABC=30°,CD⊥AB,将△ACD绕A旋转至△AC′D′,连接D′C,M、N分别是BC′和D′C的中点,连接MN,探索D′C和MN的数量及位置关系.
RT△ABC中,∠ABC=30°,CD⊥AB,将△ACD绕A旋转至△AC′D′,连接D′C,M、N分别是BC′和D′C的中点,连接MN,探索D′C和MN的数量及位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
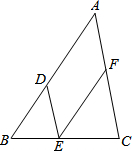 请在下列括号里填上合适的理由:
请在下列括号里填上合适的理由:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知线段AB、a、b,请用尺规按下列要求作图:
如图,已知线段AB、a、b,请用尺规按下列要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com