
分析 根据邻补角和为180度和角平分线的定义计算,再结合对顶角的性质分析得出答案.
解答 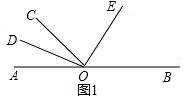 解:如图1所示,∠AOC与∠COB互为邻补角,则∠AOC+∠COB=180°,
解:如图1所示,∠AOC与∠COB互为邻补角,则∠AOC+∠COB=180°,
∵OD,OE平分∠AOC,∠COB,
∴∠COD+∠COE=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠COB=$\frac{1}{2}$180°=90°,
故互为邻补角的两个角的角平分线所成角的度数为90°;
如图2所示,∠AOD与∠DOB互为邻补角,则∠AOD+∠DOB=180°,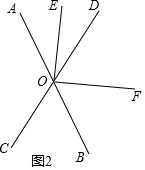
∵OE,OF平分∠AOD,∠DOB,
∴∠EOD+∠DOF=$\frac{1}{2}$∠AOD+$\frac{1}{2}$∠DOB=$\frac{1}{2}$180°=90°,
故两条相交直线所成的两对对顶角的平分线之间的夹角等于90°;
故答案为:90,90.
点评 本题主要考查了邻补角和角平分线的定义以及对顶的角的定义,正确画出图形分析是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
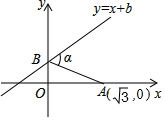 如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )
如图,已知A点坐标为($\sqrt{3}$,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=60°,则b的值为( )| A. | 3$\sqrt{3}$-3 | B. | $\sqrt{3}$+3 | C. | 2$\sqrt{3}$+3 | D. | 2$\sqrt{3}$-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
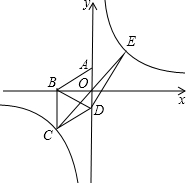 如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.
如图,在平面直角坐标系中四边形ABCD为菱形,边AD在y轴上.其中A(0,1),B(-$\sqrt{3}$,0),双曲线y=$\frac{m}{x}$经过点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,∠A=∠D=90°,AD=14,AB=4,CD=6,P是AD上的动点,连接BP,CP,若△PAB∽△CDP,则这样的点P共有( )
如图,在四边形ABCD中,∠A=∠D=90°,AD=14,AB=4,CD=6,P是AD上的动点,连接BP,CP,若△PAB∽△CDP,则这样的点P共有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com