
【题目】如图在直角坐标平面内,已知点A(﹣2,﹣3)与点B,将点A向右平移7个单位到达点C.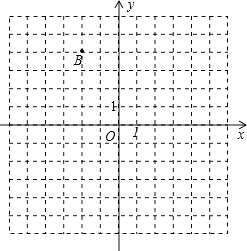
(1)点B的坐标是;A、B两点之间距离等于;
(2)点C的坐标是;△ABC的形状是;
(3)画出△ABC关于原点O对称的△A1B1C1 .
科目:初中数学 来源: 题型:
【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】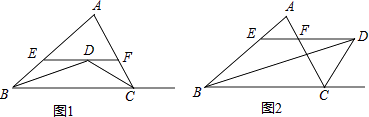
(1)如图1,在△ABC中,BD平分∠ABC,CD平分∠ACB.过D作EF∥BC交AB于E,交AC于F,请说明EF=BE+CF的理由.
(2)如图2,BD平分∠ABC,CD是△ABC中∠ACB的外角平分线,若仍然过点D作EF∥BC交AB于E,交AC于F,第(1)题的结论还成立吗?如果成立,请说明理由;如果不成立,你能否找到EF与BE、CF之间类似的数量关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮.
(1)如图1,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM:AN=8:9,问通道的宽是多少?
(2)为了建造花坛,要修改(1)中的方案,如图2,将三条通道改为两条通道,纵向的宽度改为横向宽度的2倍,其余四块草坪相同,且每一块草坪均有一边长为8m,这样能在这些草坪建造花坛.如图3,在草坪RPCQ中,已知RE⊥PQ于点E,CF⊥PQ于点F,求花坛RECF的面积.
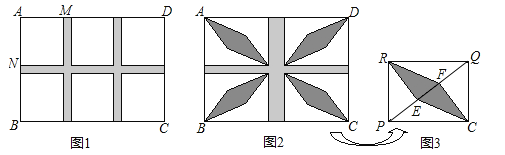
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有以下4个命题:①两条对角线互相平分的四边形是平行四边形;②两条对角线互相垂直的四边形是正方形;③两条对角线相等的四边形是菱形;④两条对角线相等且互相垂直的四边形是正方形.其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com