【题目】如图，在ABCD中，AC为对角线，AC=BC=5，AB=6，AE是△ABC的中线．
（1）用无刻度的直尺画出△ABC的高CH（保留画图痕迹）；
（2）求△ACE的面积．
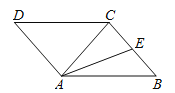
【答案】（1）作图见解析；（2）6．
【解析】（1）如图，连接BD，BD与AE交于点F，连接CF并延长到AB，则它与AB的交点即为H．
理由如下：
∵BD、AC是ABCD的对角线，∴点O是AC的中点，∵AE、BO是等腰△ABC两腰上的中线，∴AE=BO，AO=BE，∵AO=BE，∴△ABO≌△BAE（SSS），∴∠ABO=∠BAE，△ABF中，∵∠FAB=∠FBA，∴FA=FB，∵∠BAC=∠ABC，∴∠EAC=∠OBC，∵AC=BC，∠EAC=∠OBC，FA=FB，可得△AFC≌BFC（SAS），∴∠ACF=∠BCF，即CH是等腰△ABC顶角平分线，所以CH是△ABC的高；
（2）∵AC=BC=5，AB=6，CH⊥AB，∴AH=
AB=3，∴CH=
=4，∴S△ABC=ABCH=×6×4=12，∵AE是△ABC的中线，∴S△ACE=S△ABC=6．
字词句段篇系列答案科目：初中数学 来源： 题型：
【题目】据报道，目前我国“天河二号”超级计算机的运算速度位居全球第一，其运算速度达到了每秒338600000亿次，数学338600000用科学记数法可表示为（ ）
A.3.386×109
B.0.3386×109
C.33.86×107
D.3.386×108
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（ ）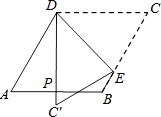 
A.78°
B.75°
C.60°
D.45°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】【问题提出】
用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？
【问题探究】
不妨假设能搭成m种不同的等腰三角形，为探究m与n之间的关系，我们可以先从特殊入手，通过试验、观察、类比、最后归纳、猜测得出结论．
【探究一】
（1）用3根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
此时，显然能搭成一种等腰三角形．
所以，当n=3时，m=1．
（2）用4根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
只可分成1根木棒、1根木棒和2根木棒这一种情况，不能搭成三角形．
所以，当n=4时，m=0．
（3）用5根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
若分成1根木棒、1根木棒和3根木棒，则不能搭成三角形．
若分成2根木棒、2根木棒和1根木棒，则能搭成一种等腰三角形．
所以，当n=5时，m=1．
（4）用6根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
若分成1根木棒、1根木棒和4根木棒，则不能搭成三角形．
若分成2根木棒、2根木棒和2根木棒，则能搭成一种等腰三角形．
所以，当n=6时，m=1．
综上所述，可得：表①
【探究二】
（1）用7根相同的木棒搭一个三角形，能搭成多少种不同的三角形？
（仿照上述探究方法，写出解答过程，并将结果填在表②中）
（2）用8根、9根、10根相同的木棒搭一个三角形，能搭成多少种不同的等腰三角形？
（只需把结果填在表②中）
表②
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究，…
【问题解决】：
用n根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（设n分别等于4k﹣1，4k，4k+1，4k+2，其中k是正整数，把结果填在表③中）
表③
【问题应用】：
用2016根相同的木棒搭一个三角形（木棒无剩余），能搭成多少种不同的等腰三角形？（写出解答过程），其中面积最大的等腰三角形每腰用了 根木棒．（只填结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
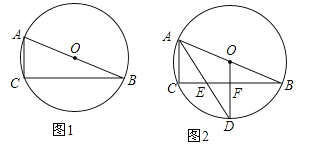
【题目】已知⊙O为△ABC的外接圆，圆心O在AB上．
（1）在图1中，用尺规作图作∠BAC的平分线AD交⊙O于D（保留作图痕迹，不写作法与证明）；
（2）如图2，设∠BAC的平分线AD交BC于E，⊙O半径为5，AC=4，连接OD交BC于F．
①求证：OD⊥BC；
②求EF的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
