
分析 根据3<$\sqrt{10}$<4,可得$\sqrt{10}$的大小,根据已知得出a、b的值,再进一步求a+b即可.
解答 解:∵3<$\sqrt{10}$<4,
∴8<5+$\sqrt{10}$<9,1<5-$\sqrt{10}$<2,
∴a=5+$\sqrt{10}$-8=$\sqrt{10}$-3,b=5-$\sqrt{10}$-1=4-$\sqrt{10}$,
∴a+b=($\sqrt{10}$-3)+(4-$\sqrt{10}$)=1;
a-b=($\sqrt{10}$-3)-(4-$\sqrt{10}$)=2$\sqrt{10}$-7.
点评 此题考查估算无理数的大小,估算出$\sqrt{10}$的大小是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+1 | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}+1$或$\sqrt{2}$-1 | D. | $\sqrt{2}$+1或$\sqrt{3}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
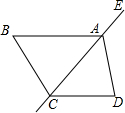 在四边形ABCD中AB∥CD,点E在CA的延长线上,若∠EAB=130°,则下列结论正确的是( )
在四边形ABCD中AB∥CD,点E在CA的延长线上,若∠EAB=130°,则下列结论正确的是( )| A. | ∠ACB=50° | B. | ∠ACD=50° | C. | ∠ADC=130° | D. | ∠EAD=130° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 某农户用5$\sqrt{11}$米长的围栏围出一块如图所示的长方形土地(墙面是长方形土地的长),已知该长方形土地的宽为$\frac{3\sqrt{11}}{2}$米,则该长方形土地的周长为7$\sqrt{11}$米.
某农户用5$\sqrt{11}$米长的围栏围出一块如图所示的长方形土地(墙面是长方形土地的长),已知该长方形土地的宽为$\frac{3\sqrt{11}}{2}$米,则该长方形土地的周长为7$\sqrt{11}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
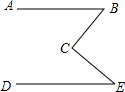 如图,AB∥DE,试问:∠B、∠E、∠BCE有什么关系.
如图,AB∥DE,试问:∠B、∠E、∠BCE有什么关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )
如图,矩形ABCD的边AB上有一点P,且AD=$\frac{5}{3}$,BP=$\frac{4}{5}$.以点P为直角顶点的直角三角形两条直角边分别交线段DC,线段BC于点E,F,连接EF,则tan∠PEF的值( )| A. | $\frac{12}{25}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com