
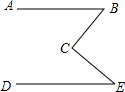
 如图,AB∥DE,试问:∠B、∠E、∠BCE有什么关系.
如图,AB∥DE,试问:∠B、∠E、∠BCE有什么关系.分析 (1)过点C作CF∥AB,由平行线的性质得出∠B=∠1,DE∥CF,得出∠E=∠2,得出∠B+∠E=∠1+∠2即可;
(2)过点C作CF∥AB,由平行线的性质得出∠B=∠1,由已知条件得出∠E=∠2,得出CF∥DE,即可得出结论.
解答 解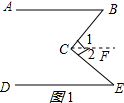 (1)∠B+∠E=∠BCE
(1)∠B+∠E=∠BCE
过点C作CF∥AB,如图所示
则∠B=∠1(两直线平行,内错角相等)
又∵AB∥DE,AB∥CF,
∴DE∥CF(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠E=∠2(两直线平行,内错角相等)
∴∠B+∠E=∠1+∠2
即∠B+∠E=∠BCE.
故答案为:1,两直线平行,内错角相等;
DE∥CF,如果两条直线都和第三条直线平行,那么这两条直线也互相平行;
2,两直线平行,内错角相等;
(2)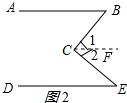 当∠B+∠E=∠BCE时,AB∥DE;理由如下:
当∠B+∠E=∠BCE时,AB∥DE;理由如下:
过点C作CF∥AB,如图2所示:
则∠B=∠1,
∵∠B+∠E=∠BCE,
∴∠E=∠2,
∴CF∥DE,
∴AB∥DE.
点评 本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质,通过作辅助线得出内错角相等是解决问题的关键.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直线PQ可能与直线AB垂直 | |
| B. | 直线PQ可能与直线AB平行 | |
| C. | 过点P的直线一定能与直线AB相交 | |
| D. | 过点Q只能画出一条直线与直线AB平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 调查了10名老年人的健康状况 | |
| C. | 在医院调查了1000名老年人的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人健康状况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com