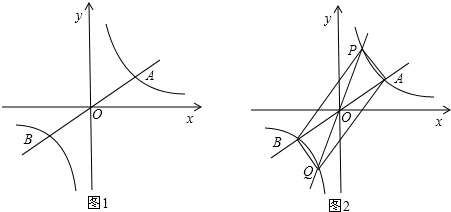
解:(1)∵双曲线和直线y=k
2x都是关于原点的中心对称图形,它们交于A,B两点,
∴B的坐标为(-4,-2),
(-m,-k
2m)或(-m,-

);
故答案为:(-4,-2);(-m,-k
2m)或(-m,-

).
(2)由勾股定理OA=
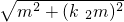
,
OB=
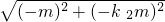
=
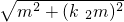
,
∴OA=OB.
同理可得OP=OQ,
所以四边形APBQ一定是平行四边形;
(3)设点A、P横坐标分别为:m,n,
由(1)可知A点坐标为(m,

),点P坐标为:(n,
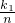
),
要OP=OA,
只要m
2+
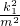
=n
2+
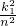
,
可得mn=k
1(∵m、n、k
1均为正数),
∴当mn=k
1时,OP=OA,
此时PQ=AB,四边形APBQ是矩形;
四边形APBQ不可能是正方形,
理由:点A,P不可能达到坐标轴,即∠POA≠90°.
分析:(1)由图象性质可知,点A、B关于坐标原点对称,由此可以求出A可求B坐标;
(2)根据勾股定理或对称性易知OA=OB,OP=OQ因此四边形APBQ一定是平行四边形;
(3)根据矩形的性质和正方形的性质可以推出它们的可能性.
点评:此题考查了反比例函数、一次函数的图形和性质,勾股定理,平行四边形的性质,矩形和正方形的性质,熟知反比例函数及正比例函数的图象均关于原点对称的特点是解答此题的关键.

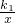 (k1>0)与直线y=k2x交于A、B两点,点A在第一象限.试解答下列问题:
(k1>0)与直线y=k2x交于A、B两点,点A在第一象限.试解答下列问题: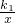 (k1>0)于P、Q两点,说明四边形APBQ是平行四边形;
(k1>0)于P、Q两点,说明四边形APBQ是平行四边形;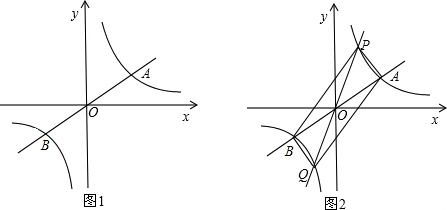
 );
); ).
).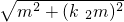 ,
,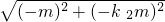 =
=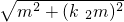 ,
, ),点P坐标为:(n,
),点P坐标为:(n,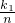 ),
),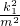 =n2+
=n2+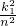 ,
,