
【题目】如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=![]() x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.
x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.
求证:四边形ABCD是矩形.
【答案】证明:作EF⊥AB于点F,
∵AB∥CD,
∴∠1=∠2,∠3=∠4,
在△ABE和△CDE中,
∴△ABE≌△CDE,
∴AE=CE,
∴四边形ABCD是平行四边形,
∵A(2,n),B(m,n),易知A,B两点纵坐标相同,
∴AB∥CD∥x轴,
∴m﹣2=4,m=6,
将B(6,n)代入直线y=![]() x+1得n=4,
x+1得n=4,
∴B(6,4),
∵CD=4=AB,△AEB的面积是2,
∴EF=1,
∵D(p,q),
∴E(![]() ,
,![]() ),F(
),F(![]() ,4),
,4),
∴![]() +1=4,
+1=4,
∴q=2,p=2,
∴DA⊥AB,
∴四边形ABCD是矩形.
【解析】首先利用对角线互相平分的四边形是平行四边形判定该四边形为平行四边形,然后根据△ABE的面积得到整个四边形的面积和AD的长,根据平行四边形的面积计算方法得当DA⊥AB即可判定矩形.
【考点精析】解答此题的关键在于理解矩形的判定方法的相关知识,掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


科目:初中数学 来源: 题型:
【题目】正方形OA1B1C1、A1A2B2C2、A2A3B3C3 , 按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=﹣x+2上,则点A3的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
A.线段AE的中垂线与线段AC的中垂线的交点
B.线段AB的中垂线与线段AC的中垂线的交点
C.线段AE的中垂线与线段BC的中垂线的交点
D.线段AB的中垂线与线段BC的中垂线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB°,AB=5,BC=3,P是AB边上的动点(不与点B重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为开展“争当书香少年”活动,小石对本校部分同学进行“最喜欢的图书类别”的问卷调查,结果统计后,绘制了如下两幅不完整的统计图:
(1)此次被调查的学生共 人
(2)补全条形统计图
(3)扇形统计图中,艺术类部分所对应的圆心角为 度
(4)若该校有1200名学生,估计全校最喜欢“文史类”图书的学生有 人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:底与腰的比是![]() 的等腰三角形叫做黄金等腰三角形.
的等腰三角形叫做黄金等腰三角形.
如图,已知△ABC中,AC=BC,∠C=36°,BA1平分∠ABC交AC于A1 . 
(1)证明:AB2=AA1AC;
(2)探究:△ABC是否为黄金等腰三角形?请说明理由;(提示:此处不妨设AC=1)
(3)应用:已知AC=a,作A1B1∥AB交BC于B1 , B1A2平分∠A1B1C交AC于A2 , 作A2B2∥AB交B2 , B2A3平分∠A2B2C交AC于A3 , 作A3B3∥AB交BC于B3 , …,依此规律操作下去,用含a,n的代数式表示An﹣1An . (n为大于1的整数,直接回答,不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(Ⅰ)求过B,C两点的抛物线y=ax2+bx﹣1解析式;
(Ⅱ)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大?最大值是多少?并说明理由.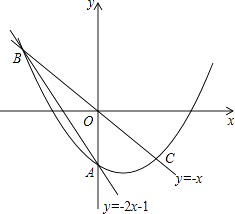
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com