
【题目】在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(Ⅰ)求过B,C两点的抛物线y=ax2+bx﹣1解析式;
(Ⅱ)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大?最大值是多少?并说明理由.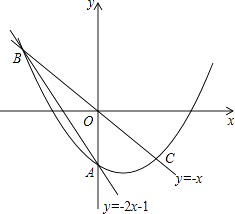
【答案】解:
(Ⅰ)联立两直线解析式可得 ![]() ,
,
解得 ![]() ,
,
∴B点坐标为(﹣1,1),
又C点为B点关于原点的对称点,
∴C点坐标为(1,﹣1),
∵直线y=﹣2x﹣1与y轴交于点A,
∴A点坐标为(0,﹣1),
设抛物线解析式为y=ax2+bx+c,
把A、B、C三点坐标代入可得 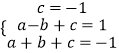 ,
,
解得 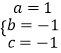 ,
,
∴抛物线解析式为y=x2﹣x﹣1;
(Ⅱ)①当四边形PBQC为菱形时,则PQ⊥BC,
∵直线BC解析式为y=﹣x,
∴直线PQ解析式为y=x,
联立抛物线解析式可得 ![]() ,
,
解得 ![]() 或
或 ![]() ,
,
∴P点坐标为(1﹣ ![]() ,1﹣
,1﹣ ![]() )或(1+
)或(1+ ![]() ,1+
,1+ ![]() );
);
②当t=0时,四边形PBQC的面积最大.
理由如下:
如图,过P作PD⊥BC,垂足为D,作x轴的垂线,交直线BC于点E,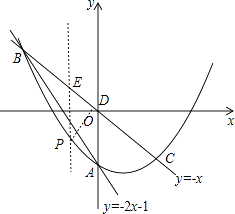
则S四边形PBQC=2S△PBC=2× ![]() BCPD=BCPD,
BCPD=BCPD,
∵线段BC长固定不变,
∴当PD最大时,四边形PBQC面积最大,
又∠PED=∠AOC(固定不变),
∴当PE最大时,PD也最大,
∵P点在抛物线上,E点在直线BC上,
∴P点坐标为(t,t2﹣t﹣1),E点坐标为(t,﹣t),
∴PE=﹣t﹣(t2﹣t﹣1)=﹣t2+1,
∴当t=0时,PE有最大值1,此时PD有最大值,即四边形PBQC的面积最大
【解析】(Ⅰ)首先求出A、B、C三点坐标,再利用待定系数法可求得抛物线解析式;(Ⅱ)①当四边形PBQC为菱形时,可知PQ⊥BC,则可求得直线PQ的解析式,联立抛物线解析式可求得P点坐标;②过P作PD⊥BC,垂足为D,作x轴的垂线,交直线BC于点E,由∠PED=∠AOC,可知当PE最大时,PD也最大,用t可表示出PE的长,可求得取最大值时的t的值.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=![]() x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.
x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.
求证:四边形ABCD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了三角形全等的判定方法和直角三角形全等的判定方法后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情况进行研究.
(初步思考)我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,![]() ,然后,对
,然后,对![]() 进行分类,可分为“
进行分类,可分为“![]() 是直角,钝角,锐角”三种情况进行探索.
是直角,钝角,锐角”三种情况进行探索.
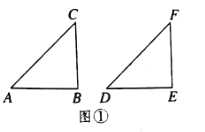
(深入探究)(1)当![]() 是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF,
是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF,![]() ,根据 可以知道
,根据 可以知道![]() .
.
(2)当![]() 是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF,
是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF,![]() ,且
,且![]() 都是钝角,求证:
都是钝角,求证:![]() .
.
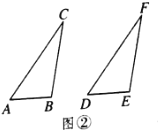
(3)当![]() 是锐角时,在△ABC和△DEF中,AC=DF,BC=EF,
是锐角时,在△ABC和△DEF中,AC=DF,BC=EF,![]() ,且
,且![]() 都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)
都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,则HD的长为 .
,则HD的长为 . 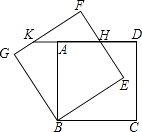
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E. 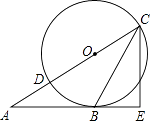
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,H,G,N在同一直线上,△EFG≌△NMH,∠F和∠M是对应角.在△EFG中,FG是最长边.在△NMH中,MH是最长边.已知EF=2.1 cm,EH=1.1 cm,HN=3.3 cm.
(1)写出其他对应边及对应角;
(2)求线段MN及线段HG的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑车从家出发,先向东骑行1km到达A村,继续向东骑行4km到达B村,然后向西骑行8km到达C村,最后回到家.
(1) 以快递公司为原点,以向东方向为正方向,用1 cm表示1 km,画出数轴,并在数轴上表示出A、B、C三个店的位置;
(2) C店离A店有多远?
(3) 快递员一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
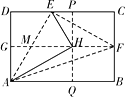
【题目】如图,矩形纸片ABCD中,G、F分别为AD、BC的中点,将纸片折叠,使D点落在GF上,得到△HAE , 再过H点折叠纸片,使B点落在直线AB上,折痕为PQ.连接AF、EF , 已知HE=HF.下列结论:①△MEH为等边三角形;②AE⊥EF;③△PHE∽△HAE;④![]() ,
, 
其中正确的结论是
A.①②③
B.①②④
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com