
【题目】如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E. 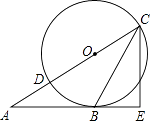
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
【答案】
(1)证明:如图1,连接OB,
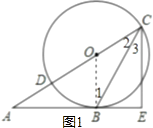
∵AB是⊙0的切线,
∴OB⊥AB,
∵CE丄AB,
∴OB∥CE,
∴∠1=∠3,
∵OB=OC,
∴∠1=∠2,
∴∠2=∠3,
∴CB平分∠ACE
(2)解:如图2,连接BD,
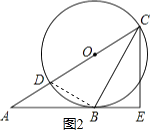
∵CE丄AB,
∴∠E=90°,
∴BC= ![]() =
= ![]() =5,
=5,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC,
∴△DBC∽△CBE,
∴ ![]() ,
,
∴BC2=CDCE,
∴CD= ![]() =
= ![]() ,
,
∴OC= ![]() =
= ![]() ,
,
∴⊙O的半径= ![]() .
.
【解析】(1)证明:如图1,连接OB,由AB是⊙0的切线,得到OB⊥AB,由于CE丄AB,的OB∥CE,于是得到∠1=∠3,根据等腰三角形的性质得到∠1=∠2,通过等量代换得到结果.(2)如图2,连接BD通过△DBC∽△CBE,得到比例式 ![]() ,列方程可得结果.
,列方程可得结果.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
A.线段AE的中垂线与线段AC的中垂线的交点
B.线段AB的中垂线与线段AC的中垂线的交点
C.线段AE的中垂线与线段BC的中垂线的交点
D.线段AB的中垂线与线段BC的中垂线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y= ![]() 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y= ![]() 的图象上,则k的值为( )
的图象上,则k的值为( ) 
A.﹣4
B.4
C.﹣2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,直线y=﹣2x﹣1与y轴交于点A,与直线y=﹣x交于点B,点B关于原点的对称点为点C.
(Ⅰ)求过B,C两点的抛物线y=ax2+bx﹣1解析式;
(Ⅱ)P为抛物线上一点,它关于原点的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②若点P的横坐标为t(﹣1<t<1),当t为何值时,四边形PBQC面积最大?最大值是多少?并说明理由.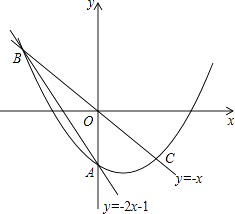
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,用尺规作∠ABC=90°,作法如下:
小明的作法:(1)分别以A、B为圆心AB长为半径画弧,两弧交于点P;(2)以P为圆心,AB长为半径画弧交AP的延长线于C;连接AC,则∠ABC=90° |
|
(1)请证明∠ABC=90°;
(2)请你用不同的方法,用尺规作∠ABC=90°.
(要求:保留作图痕迹,不写作法,并用2B铅笔把作图痕迹描粗)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在海湾森林公园放风筝.如图所示,小明在A处,风筝飞到C处,此时线长BC为40米,若小明双手牵住绳子的底端B距离地面1.5米,从B处测得C处的仰角为60°,求此时风筝离地面的高度CE.(计算结果精确到0.1米, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com