
【题目】如图,点C是线段AB的中点,CD平分![]() ,CE平分
,CE平分![]() ,CD=CE.
,CD=CE.
(1)求证:![]()
(2)若![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)见解析;(2)67°
【解析】
(1)根据角平分线的定义得到∠ACD=∠BCE,由C是线段AB的中点,得到AC=BC.根据全等三角形的判定定理即可得到结论;
(2)根据平角的定义得到∠ACD=∠DCE=∠BCE=60°,根据全等三角形的性质得到∠E=∠D=53°,根据三角形的内角和即可得到结论.
(1)证明:![]() CD平分∠ACE,
CD平分∠ACE,
![]() ∠ACD=∠DCE,
∠ACD=∠DCE,
![]() CE平分∠BCD,
CE平分∠BCD,
![]() ∠DCE=∠BCE,
∠DCE=∠BCE,
![]() ∠ACD=∠BCE,
∠ACD=∠BCE,
![]() C是线段AB的中点,
C是线段AB的中点,
![]() AC=BC.
AC=BC.
在△ACD与△BCE中,
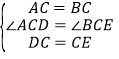
![]() △ACD≌△BCE;
△ACD≌△BCE;
(2) ![]() ∠ACD=∠DCE=∠BCE=
∠ACD=∠DCE=∠BCE=![]() ×180°=60°,
×180°=60°,
![]() △ACD≌△BCE,
△ACD≌△BCE,
![]() ∠E=∠D=53°,
∠E=∠D=53°,
![]() ∠B=180°60°53°=67°.
∠B=180°60°53°=67°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D,E,F,G,已知∠CGD=42°
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示,点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展校园“美德少年”评选活动,共有“助人为乐”,“自强自立”、“孝老爱亲”,“诚实守信”四种类别,每位同学只能参评其中一类,评选后,把最终入选的20位校园“美德少年”分类统计,制作了如下统计表,后来发现,统计表中前两行的数据都是正确的,后两行的数据中有一个是错误的.
类别 | 频数 | 频率 |
助人为乐美德少年 | a | 0.20 |
自强自立美德少年 | 3 | b |
孝老爱亲美德少年 | 7 | 0.35 |
诚实守信美德少年 | 6 | 0.32 |
根据以上信息,解答下列问题:
(1)统计表中的a= ,b ;
(2)统计表后两行错误的数据是 ,该数据的正确值是 ;
(3)校园小记者决定从A,B,C三位“自强自立美德少年”中随机采访两位,用画树状图或列表的方法,求A,B都被采访到的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=18米,![]() 于点A,MA=6米,射线
于点A,MA=6米,射线![]() 于点B,P点从B点出发向A运动,每秒走1米,Q点从B点向D点运动,每秒走2米,P,Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
于点B,P点从B点出发向A运动,每秒走1米,Q点从B点向D点运动,每秒走2米,P,Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )

A. 4 B. 6 C. 4或9 D. 6或9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,![]() 且
且![]() 于点E,与CD相交于点F,
于点E,与CD相交于点F,![]() 于点H,交BE于点G.下列结论:①BD=CD;②AD+CF=BD;③
于点H,交BE于点G.下列结论:①BD=CD;②AD+CF=BD;③![]() ;④AE=CF.其中正确的是____________(填序号)
;④AE=CF.其中正确的是____________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
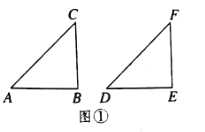
【题目】学习了三角形全等的判定方法和直角三角形全等的判定方法后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情况进行研究.
(初步思考)我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,![]() ,然后,对
,然后,对![]() 进行分类,可分为“
进行分类,可分为“![]() 是直角,钝角,锐角”三种情况进行探索.
是直角,钝角,锐角”三种情况进行探索.
(深入探究)(1)当![]() 是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF,
是直角时,如图①,在△ABC和△DEF中,AC=DF,BC=EF,![]() ,根据 可以知道
,根据 可以知道![]() .
.
(2)当![]() 是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF,
是钝角时,如图②,在△ABC和△DEF中,AC=DF,BC=EF,![]() ,且
,且![]() 都是钝角,求证:
都是钝角,求证:![]() .
.
(3)当![]() 是锐角时,在△ABC和△DEF中,AC=DF,BC=EF,
是锐角时,在△ABC和△DEF中,AC=DF,BC=EF,![]() ,且
,且![]() 都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)
都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等(不写做法,保留作图痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某油箱容量为60 L的汽车,加满汽油后行驶了100 Km时,油箱中的汽油大约消耗了![]() ,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
,如果加满汽油后汽车行驶的路程为x Km,邮箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
A. y=0.12x,x>0 B. y=60﹣0.12x,x>0 C. y=0.12x,0≤x≤500 D. y=60﹣0.12x,0≤x≤500
查看答案和解析>>
科目:初中数学 来源: 题型:
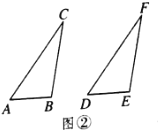
【题目】如图,已知三角形ABC的边AB是⊙0的切线,切点为B.AC经过圆心0并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E. 
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于A(﹣1,0)、B(3,0)、C(0,3)三点.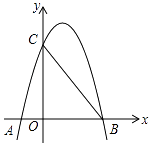
(1)试求抛物线的解析式;
(2)P是直线BC上方抛物线上的一个动点,设P的横坐标为t,P到BC的距离为h,求h与t的函数关系式,并求出h的最大值.
(3)设点M是x轴上的动点,在平面直角坐标系中,是否存在点N,使得以点A、C、M、N为顶点的四边形是菱形?若存在,求出所有符合条件的点N坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com