
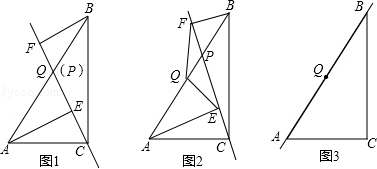
分析 (1)首先证明△BFQ≌△AEQ可得QE=QF,再由AQ=BQ可利用对角线互相平分的四边形是平行四边形判定四边形AEBF是平行四边形;
(2)首先证明△FBQ≌△DAQ可得QF=QD,再根据直角三角形斜边中线等于斜边的一半可得QE=QF=QD,进而可得结论.
解答 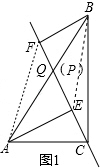 证明:(1)如图1,∵Q为AB中点,
证明:(1)如图1,∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,∠BFQ=∠AEQ,
在△BFQ和△AEQ中:$\left\{\begin{array}{l}{∠BFQ=∠AEQ}\\{∠BQF=∠AQE}\\{BQ=AQ}\end{array}\right.$
∴△BFQ≌△AEQ(AAS),
∴QE=QF,
∴四边形AEBF是平行四边形;
(2)QE=QF,
如图2,延长FQ交AE于D,
∵AE∥BF,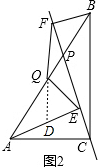
∴∠QAD=∠FBQ,
在△FBQ和△DAQ中$\left\{\begin{array}{l}{∠FBQ=∠DAQ}\\{AQ=BQ}\\{∠BQF=∠AQD}\end{array}\right.$,
∴△FBQ≌△DAQ(ASA),
∴QF=QD,
∵AE⊥CP,
∴EQ是直角三角形DEF斜边上的中线,
∴QE=QF=QD,即QE=QF,
∴△QEF是等腰三角形.
点评 此题主要考查了平行四边形的判定,直角三角形的性质,全等三角形的判定和性质,关键是掌握对角线互相平分的四边形是平行四边形.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:选择题
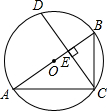 如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )
如图,⊙O的直径AB垂直于弦CD,垂足为E.若∠B=60°,AC=3,则CD的长为( )| A. | 6 | B. | $2\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为20$\sqrt{2}$海里.
如图,在某监测点B 处望见一艘正在作业的渔船在南北偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B,C之间的距离为20$\sqrt{2}$海里.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=60°,分别以△ABC的两边向形外作等边△BCE、等边△ACF,过A作AM∥FC交BC于点M,连接EM.
如图,△ABC中,∠ACB=60°,分别以△ABC的两边向形外作等边△BCE、等边△ACF,过A作AM∥FC交BC于点M,连接EM.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com