
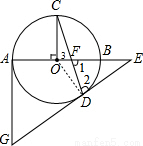
如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
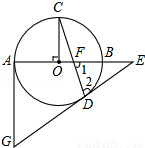
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
(1)见解析;(2)AG=6.
【解析】
试题分析:(1)连接OD,根据切线的性质可得∠2+∠ODC=90°,根据OC=OD可得∠C=∠ODC,结合条件OC⊥AB,利用互余的关系可证∠1=∠2;(2)根据条件OF:OB=1:3,⊙O的半径为3,可得OF=1,由(1)可得EF=ED,设DE=x,在Rt△ODE中,由勾股定理可得x=4,然后利用Rt△EOD∽Rt△EGA,可求出AG=6.
试题解析:(1)证明:连接OD,∵DE为⊙O的切线,
∴OD⊥DE,∴∠ODE=90°,即∠2+∠ODC=90°,∵OC=OD,
∴∠C=∠ODC,∴∠2+∠C=90°,而OC⊥OB,∴∠C+∠3=90°,
∴∠2=∠3,∵∠1=∠3,∴∠1=∠2; 4分
(2)【解析】
∵OF:OB=1:3,⊙O的半径为3,∴OF=1,∵∠1=∠2,∴EF=ED,
在Rt△ODE中,OD=3,DE=x,则EF=x,OE=1+x,
∵OD2+DE2=OE2,∴32+x2=(x+1)2,解得x=4, 7分
∴DE=4,OE=5,∵AG为⊙O的切线, ∴AG⊥AE,∴∠GAE=90°,
而∠OED=∠GEA,∴Rt△EOD∽Rt△EGA,
∴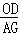 =
=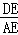 ,即
,即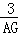 =
=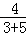 ,∴AG=6. 10分
,∴AG=6. 10分
考点:1.切线的性质;2.互余;3.勾股定理;4.相似三角形的判定与性质.


科目:初中数学 来源:2014-2015学年山东省诸城市九年级下学期开学检测数学试卷(解析版) 题型:填空题
关于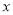 的一元二次方程
的一元二次方程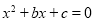 的两个根为
的两个根为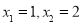 ,那么抛物线
,那么抛物线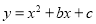 的
的
顶点坐标为_____________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期期末考试数学试卷(解析版) 题型:选择题
已知函数y=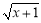 ,则自变量x的取值范围是( )
,则自变量x的取值范围是( )
A.x<-1 B.x>-1 C.x≤-1 D.x≥-1
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:选择题
二次函数y=ax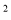 +bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)
+bx+c(a≠0)的图象如图所示,下列结论:①c<0,②b>0,③4a+2b+c>0,④(a+c)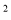 <b
<b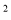 ,其中正确的有( )
,其中正确的有( )
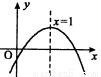
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省铜陵市四校九年级2月开学联考数学试卷(解析版) 题型:选择题
下列事件为必然事件的是( )
A.小王参加本次数学考试,成绩是150分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,中央一套节目正在播新闻
D.口袋中装有两个红球和一个白球,从中摸出两个球,其中必有红球
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市毕业班正月联考数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=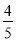 .下列结论:
.下列结论:
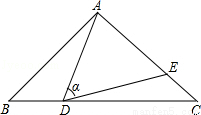
①△ADE∽△ACD;
②当BD=6时,△ABD与△DCE全等;
③△DCE为直角三角形时,BD为8或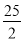 ;
;
④0<CE≤6.4.
其中正确的结论是 _________ .(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省安庆市毕业班正月联考数学试卷(解析版) 题型:选择题
拦水坝横断面如图所示,迎水坡AB的坡比是1: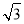 ,坝高BC=10m,则坡面AB的长度是( )
,坝高BC=10m,则坡面AB的长度是( )
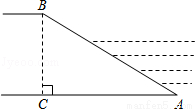
A.15m B.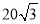 m C.
m C.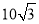 m D.20m
m D.20m
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市七年级上学期期中考试数学试卷(解析版) 题型:选择题
已知代数式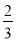 x2-x+1的值是2,则代数式2x2-3x的值是( )
x2-x+1的值是2,则代数式2x2-3x的值是( )
A.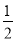 B. 9 C.6 D.3
B. 9 C.6 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com