Question

（本题满分10分）如图1，在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，点D是BC上一定点．动点P从C出发，以2cm/s的速度沿C→A→B方向运动，动点Q从D出发，以1cm/s的速度沿D→B方向运动．点P出发5 s后,点Q才开始出发，且当一个点达到B时，另一个点随之停止．图2是当时△BPQ的面积S（ cm2）与点P的运动时间t（s）的函数图象．

（1）CD = , ；

（2）当点P在边AB上时，为何值时，使得△BPQ与△ABC为相似？

（3）运动过程中，求出当△BPQ是以BP为腰的等腰三角形时的值．

 

Answer 1

（1）2 10．8 （2）或6 （3）5、

【解析】

试题分析：（1）根据函数图象得到当点P运动到点A时，△BPQ的面积为18，利用三角形面积公式可计算出BD=6，则CD=2，当t=5s时，AP=4，点Q在D点，作PH⊥BC于H，在Rt△ABC中根据勾股定理计算出AB=10，再证明△BPH∽△BAC，利用相似比计算出PH，然后根据三角形面积公式得到S△PBQ，即a=S△PBQ；

（2）分类讨论：当3＜t≤5，点Q在D点，BP=16-2t，若PD⊥BC得到△BPQ∽△BAC，利用相似比得t值；当5＜t≤8，DQ=t-5，BQ=11-t，BP=16-2t，当∠PQB=90°时，△BPQ∽△BAC，利用相似比得t值；当∠BPQ=90°时，△BPQ∽△BAC，利用相似比得t值；

（3）PB=16-2t，BQ=11-t，分类讨论：当BP=BQ，则16-2t=11-t，解方程得t=5；当PB=PQ，作PM⊥BC于M，根据等腰三角形的性质得则BM=BQ=（11-t），再证明△BPM∽△BAC，利用相似比得t值．

试题解析：（1）当点P运动到点A时，△BPQ的面积为18，

∴×6•BD=18，解得BD=6，

∴CD=BC-BD=2，

当t=5s时，AP=2×5-6=4，点Q在D点，点P在AB上如图①，作PH⊥BC于H，

在Rt△ABC中，AC=6，BC=8，

∴AB==10，

∵PH∥AC，

∴△BPH∽△△BAC，

∴，即，解得PH=

∴S△PBQ=×6×=

即a=

故答案为：2，；

（2）点P在边AB上，

当3＜t≤5，点Q在D点，BP=16-2t，

若PD⊥BC，△BPQ∽△BAC，

∴，即，解得t=；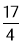

当5＜t≤8，DQ=t-5，则BQ=8-2-（t-5）=11-t，BP=16-2t，

当∠PQB=90°时，△BPQ∽△BAC，如图②，

∵△BPQ∽△BAC，

∴=，即=，解得t=3，不合题意舍去；

当∠BPQ=90°时，△BPQ∽△BAC，如图③，

∵△BPQ∽△BCA，

∴，即，解得t=6，

综上所述，当t为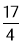或6时，△BPQ与△ABC为相似；

 

（3）PB=16-2t，BQ=11-t，

当BP=BQ，则16-2t=11-t，解得t=5；

当PB=PQ，作PM⊥BC于M，如图④，

则BM=BQ=（11-t），

∵PM∥AC，

∴△BPM∽△BAC，

∴，即，解得t=，

综上所述，当△BPQ是以BP为腰的等腰三角形时t的值为5或．

考点：函数图象与性质，等腰三角形，相似三角形，勾股定理