
【题目】如图,△ABC中,点E、P在边AB上,且AE=BP,过点E、P作BC的平行线,分别交AC于点F、Q.记△AEF的面积为![]() ,四边形EFQP的面积为
,四边形EFQP的面积为![]() ,四边形PQCB的面积为
,四边形PQCB的面积为![]()
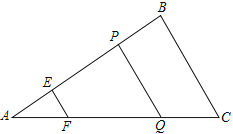
(1)求证:EF+PQ=BC
(2)若![]() +
+![]() =
=![]() ,求
,求![]() 的值
的值
(3)若![]() -
-![]() =
=![]() ,直接写出
,直接写出![]() 的值
的值
【答案】见解析;2;![]() .
.
【解析】
试题过点Q作QD∥PB,从而得到四边形PQDB为平行四边形,根据平行四边形性质得到PQ=BD,PB=QD,∠B=∠QDC,然后再证明△AEF和△QDC全等,从而得出答案;过点A作AH⊥BC于H,分别交EF、PQ于M、N,设EF=a,PQ=b,AM=h,则BC=a+b,根据三角形相似得出![]() ,从而求出AN和MN的长度,然后分别求出
,从而求出AN和MN的长度,然后分别求出![]() 、
、![]() 和
和![]() 的代数式,然后根据三者之间的关系求出a和b的关系,然后得出答案;根据(2)的同样方法得出答案.
的代数式,然后根据三者之间的关系求出a和b的关系,然后得出答案;根据(2)的同样方法得出答案.
试题解析:(1)如图所示,过点Q作QD∥PB
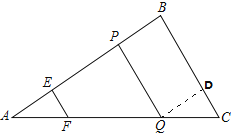
∵PQ∥BC,QD∥BP ∴四边形PQDB为平行四边形 ∴PQ=BD,PB=QD ∠B=∠QDC
∵AE=BP ∴AE=QD ∵EF∥BC ∴∠AFE=∠C ∠AEF=∠B ∴∠AEF=∠QDC
∴△AEF≌△QDC ∴EF=CD ∴BC=BD+CD=PQ+EF
(2)如图,过点A作AH⊥BC于H,分别交EF、PQ于M、N,
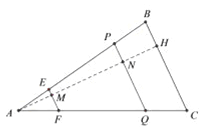
设EF=a,PQ=b,AM=h,则BC=a+b ∵![]() ∴AN=
∴AN=![]() h MN=(
h MN=(![]() -1)h
-1)h
则:![]() =
=![]() ah
ah![]() =
=![]() (a+b)(
(a+b)(![]() -1)h
-1)h![]() =
=![]() (b+a+b)h
(b+a+b)h
∵![]() +
+![]() =
=![]() ∴
∴![]() ah+
ah+![]() (b+a+b)h=
(b+a+b)h=![]() (a+b)(
(a+b)(![]() -1)h ∴b=3a ∴
-1)h ∴b=3a ∴![]() =2
=2
(3)![]()


科目:初中数学 来源: 题型:
【题目】边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2![]() .
.
(1)如图1,将△DEC沿射线EC方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.
(2)如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P.
①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
②连接AP,当AP最大时,求AD′的值.(结果保留根号)
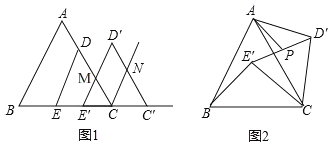
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且
与x轴相交于A(3,0)、B两点,与y轴交于点C(0,3),点B在x轴的负半轴上,且![]() .
.

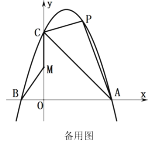
(1)求抛物线的函数关系式;
(2)若P是抛物线上且位于直线![]() 上方的一动点,求
上方的一动点,求![]() 的面积的最大值及此时点P的坐标;
的面积的最大值及此时点P的坐标;
(3)在线段![]() 上是否存在一点M,使
上是否存在一点M,使![]() 的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.
的值最小?若存在,请求出这个最小值及对应的M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.
(1)问:今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕点A逆时针旋转,使AB与AC重合,点D旋转到点E,则∠CDE的正切值为 .
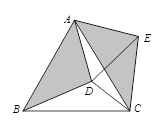
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A在y轴上,∠OAB=30°,B(2,0),OC⊥AB于点C,点C在反比例函数y=![]() (k≠0)的图象上.
(k≠0)的图象上.
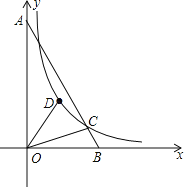
(1)求该反比例函数解析式;
(2)若点D为反比例函数y=![]() (k≠0)在第一象限的图象上一点,且∠DOC=30°,求点D的坐标.
(k≠0)在第一象限的图象上一点,且∠DOC=30°,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,已知正方形ABCD和正方形AEFG,连接DG,BE.
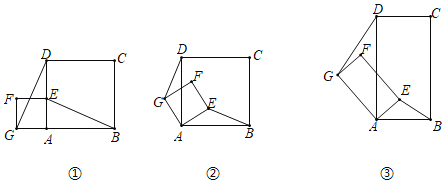
(1)发现:当正方形AEFG绕点A旋转,如图②所示.
①线段DG与BE之间的数量关系是 ;
②直线DG与直线BE之间的位置关系是 ;
(2)探究:如图③所示,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE时,上述结论是否成立,并说明理由.
(3)应用:在(2)的情况下,连接BG、DE,若AE=1,AB=2,求BG2+DE2的值(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A在第一象限,![]() 轴于B点,连结
轴于B点,连结![]() ,将
,将![]() 折叠,使
折叠,使![]() 点落在x轴上,折痕交
点落在x轴上,折痕交![]() 边于D点,交斜边
边于D点,交斜边![]() 于E点,(1)若A点的坐标为
于E点,(1)若A点的坐标为![]() ,当
,当![]() 时,点
时,点![]() 的坐标是______;(2)若
的坐标是______;(2)若![]() 与原点O重合,
与原点O重合,![]() ,双曲线
,双曲线![]() 的图象恰好经过D,E两点(如图2),则
的图象恰好经过D,E两点(如图2),则![]() ____.
____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com