
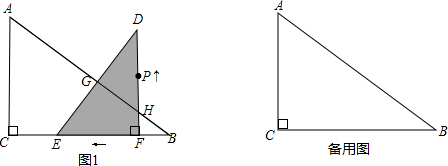
 点C时,△DEF和点P同时停止运动.设运动的时间是t(单位:s),t>0.
点C时,△DEF和点P同时停止运动.设运动的时间是t(单位:s),t>0. ,DG=
,DG=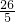 ;
;
 .
. 时△PDE为等腰三角形;
时△PDE为等腰三角形; =
=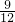 =
= ,tanD=
,tanD=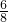 =
= ,
, t,DH=DF-FH=8-
t,DH=DF-FH=8- t,DG=DH•cosD=(8-
t,DG=DH•cosD=(8- t)•
t)• =-
=- t+
t+ ,
, t+
t+ ,解得t=
,解得t=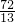 ,
,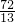 <6,则此时点P在DE边上.
<6,则此时点P在DE边上.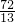 时,点P与点G重合.
时,点P与点G重合. =2.
=2. ;
;
 •(18-2t)=-
•(18-2t)=- t+
t+ ,ES=PE•sin∠EPS=PE•sinD=
,ES=PE•sin∠EPS=PE•sinD= •(18-2t)=-
•(18-2t)=- t+
t+ ,
, t+
t+ )=
)=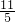 t-
t- ,
, =
= ,
, .
. .
. ,则FH=
,则FH= t,DH=8-
t,DH=8- t,得到DG=-
t,得到DG=- t+
t+ ,而DP+DF=2t,于是有2t-8=-
,而DP+DF=2t,于是有2t-8=- t+
t+ ,即可解得t的值;
,即可解得t的值; =2;当4<t≤6时,点P在DE边上运动,作PS⊥BC于S,PE=DE-DP=10-(2t-8)=18-2t.tan∠PBF=
=2;当4<t≤6时,点P在DE边上运动,作PS⊥BC于S,PE=DE-DP=10-(2t-8)=18-2t.tan∠PBF= =
= .
.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
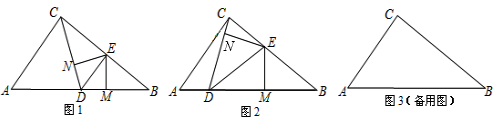
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| OC2 |
| 1 |
| OD2 |
| 1 |
| OM2 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| h2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
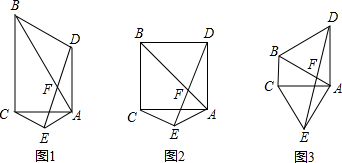
查看答案和解析>>
科目:初中数学 来源: 题型:
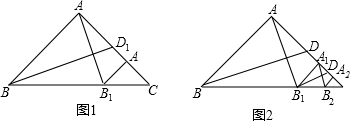
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com