
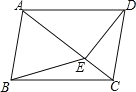
【题目】如图,在四边形 ABCD 中,AB∥CD,∠ABC=∠ADC,DE⊥AC,垂足为 E.连接 BE
(1)求证:在四边形 ABCD 是平行四边形
(2)若△ABE 是等边三角形,四边形 BCDE 的面积等于 4![]() ,求 AE 的长.
,求 AE 的长.
【答案】(1)证明见解析;(2)4.
【解析】(1)可利用两组对角分别相等的四边形是平行四边形进行证明;
(2)利用同底等高说明△CED与△CEB的面积关系,再根据四边形的面积得到△CED的面积,求出边长CD,即可得出结论.
(1)∵AB∥CD,∴∠DAB+∠ADC=∠ABC+∠BCD=180°.
∵∠ABC=∠ADC,∴∠DAB=∠BCD,∴四边形ABCD是平行四边形;
(2)∵AB∥CD,∴∠BAC=∠ACD.
∵△ABE是等边三角形,∴AB=AE=CD,∠BAC=∠ACD=60°.在Rt△CDE中,设CD的长为a,则CE=![]() a,DE=
a,DE=![]() ,S△CED=
,S△CED=![]() .
.
因为△CED与△CEB是同底等高的三角形,∴S△CED=S△CEB.又∵S四边形BCDE=S△CED+S△CEB=4![]() ,∴S△CED=
,∴S△CED=![]() .即
.即![]() =
=![]() .
.
所以a=4.即AE= CD=4.


科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB内部有三条射线,其中OE平分角∠BOC,OF平分∠AOC.
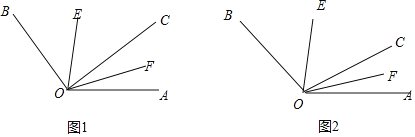
(1)如图1,若∠AOB=120°,∠AOC=30°,求∠EOF的度数?
(2)如图2,若∠AOB=α,求∠EOF的度数,(用含α的式子表示)
(3)若将题中的“平分”的条件改为“∠EOB=![]() ∠COB,∠COF=
∠COB,∠COF=![]() ∠COA,且∠AOB=α,求∠EOF的度数.(用含α的式子表示)
∠COA,且∠AOB=α,求∠EOF的度数.(用含α的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
某管道由甲、乙两工程队单独施工分别需要30天、20天.
(1)如果两队从管道两端同时施工,需要多少天完工?
(2)又知甲队单独施工每天需付200元施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施工,还是由乙队单独施工,还是由两队同时施工?请你按照少花钱多办事的原则,设计一个方案,并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时。其它主要参考数据如下:
运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费用(元) |
火车 | 100 | 15 | 2000 |
汽车 | 80 | 20 | 900 |
(1)如果汽车的总支出费用比火车费用多1100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与某市之间的距离为S千米,且知道火车与汽车在路上耽误的时间分别为2小时和3.1小时,你若是某市水果批发部门的经理,要将这种水果从A市运往本市销售。你将选择哪种运输方式比较合算呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在圣诞节来临之际,某儿童商场用2800元购进了一批玩具,上市后很快售完,商场又用7200元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个玩具进价多了4元.
(1)该商场两次共购进这批玩具多少个?
(2)如果这两批玩具每个的售价相同,且全部售完后总利润率不低于20%,那么每个玩具的售价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com