
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() 分别切⊙
分别切⊙![]() 于点
于点![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() 的延长线交⊙
的延长线交⊙![]() 于点
于点![]() 于点
于点![]() .
.
⑴求证![]() ;
;
⑵若![]() ,求
,求![]() 的长.
的长.
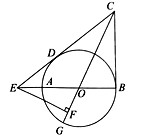
【答案】(1);(2).
【解析】
试题分析:(1)利用切线长定理得到OC平分∠BCE,即∠ECO=∠BCO,利用切线的性质得OB⊥BC,则∠BCO+∠COB=90°,由于∠FEB+∠FOE=90°,∠COB=∠FOE,所以∠FEB=∠ECF;
(2)连接OD,如图,利用切线长定理和切线的性质得到CD=CB=6,OD⊥CE,则CE=10,利用勾股定理可计算出BE=8,设⊙O的半径为r,则OD=OB=r,OE=8﹣r,在Rt△ODE中,根据勾股定理得r2+42=(8﹣r)2,解得r=3,所以OE=5,OC=3![]() ,然后证明△OEF∽△OCB,利用相似比可计算出EF的长.
,然后证明△OEF∽△OCB,利用相似比可计算出EF的长.
试题解析(1)证明:∵CB,CD分别切⊙O于点B,D,
∴OC平分∠BCE,即∠ECO=∠BCO,OB⊥BC,∴∠BCO+∠COB=90°,
∵EF⊥OG,∴∠FEB+∠FOE=90°,而∠COB=∠FOE,∴∠FEB=∠ECF;
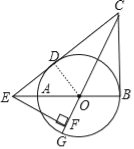
(2)解:连接OD,如图,
∵CB,CD分别切⊙O于点B,D,∴CD=CB=6,OD⊥CE,∴CE=CD+DE=6+4=10,
在Rt△BCE中,BE=![]() =8,
=8,
设⊙O的半径为r,则OD=OB=r,OE=8﹣r,
在Rt△ODE中,r2+42=(8﹣r)2,解得r=3,
∴OE=8﹣3=5,
在Rt△OBC中,OC=![]() =3
=3![]() ,
,
∵∠COB=∠FOE,∴△OEF∽△OCB,
∴![]() ,即
,即![]() ,∴EF=2
,∴EF=2![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF. 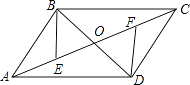
(1)求证:△BOE≌△DOF;
(2)连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为满足同学们课外活动的需求,要求购排球和足球若干个.已知足球的单价比排球的单价多![]() 元,用
元,用![]() 元购得的排球数量与用
元购得的排球数量与用![]() 元购得的足球数量相等.
元购得的足球数量相等.
⑴排球和足球的单价各是多少元?
⑵若恰好用去![]() 元,有哪几种购买方案?
元,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.

(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是( ) 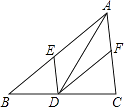
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD⊥BC,那么四边形AEDF是菱形
D.如果AD平分∠BAC,那么四边形AEDF是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com