下列变形中.属因式分解的是( )A．2x-2y=2(x-y)B．(x+y)2=x2+2xy+y2C．=x2-2y2D．x2-4x+5=(x-2)2+1 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

10．下列变形中，属因式分解的是（　　）

A．

2x-2y=2（x-y）

B．

（x+y）²=x²+2xy+y²

C．

（x+2y）（x-2y）=x²-2y²

D．

x²-4x+5=（x-2）²+1

分析根据因式分解的定义：就是把整式变形成整式的积的形式，即可作出判断．

解答解：A、2x-2y=2（x-y）是因式分解，故选项正确；
B、（x+y）²=x²+2xy+y²结果不是积的形式，不是因式分解，故选项错误；
C、（x+2y）（x-2y）=x²-4y²是整式的乘法，不是因式分解，故选项错误；
D、x²-4x+5=（x-2）²+1，结果不是积的形式，不是因式分解，故选项错误．
故选A．

点评本题主要考查了因式分解的意义，因式分解是整式的变形，变形前后都是整式，并且结果是积的形式．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

17．

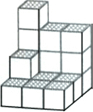如图，在一次数学活动课上，张明用17个边长为1的小正方体搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要19个小立方体，王亮所搭几何体的表面积为48．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

1．

已知：如图，在△ABC中，∠BAC=90°，AH⊥BC于H，以AB和AC为边在Rt△ABC外作等边△ABD和△ACE，求证：DH⊥HE．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

18．阅读下面例题的分析与解答，再回答问题：
例：已知x+y=6，xy=2，求x²+y²的值
分析：问题中有x²和y²，但已经条件中并没有平方项，因而需要从已知条件中变形出x²和y²行．若将两个已知等式两边分别相乘，得xy（x+y）=12解题．联想到完全公式，若将第一等式分别平方则可出现x²和y²再将第二个等式代入即可解决这个问题．
解：∵x+y=6
∴（x+y）²=6²
即x²+2xy+y²=36
∵xy=2
∴x²+2x×2+y²=36
∴x²+y²=32
作出什么样变形或者需要先要求出什么式子的值才能进行下一步．这需要我们联想相关的公式和类似的已经会做的题型．
问题一：
（1）若已知x+$\frac{1}{x}$=3，求x²+$\frac{1}{{x}^{2}}$和x⁴+$\frac{1}{{x}^{4}}$的值；
（2）若已经x²-5x+1=0，则x²+$\frac{1}{{x}^{2}}$=23；
问题二：若10^a=20，10^b=$\frac{1}{5}$，求9^a÷3^2b的值．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．按下列要求作图：
（1）在正方形网格中三条不同实线上各取一个格点，使其中任意两点，不在同一实线上．
（2）连结三个格点，使之构成直角三角形（如图1），请在图2网格中作出三个直角三角形，使四个直角三角形互不全等．