
【题目】如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( ) 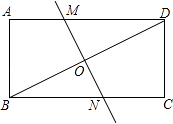
A.![]()
B.![]()
C.![]()
D.2 ![]()
【答案】B
【解析】解:如图,连接BM,DN
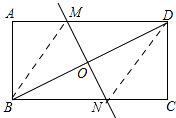
在矩形纸片ABCD中,CD=AB=2,∠C=90°,
在Rt△BCD中,BC=4,
根据勾股定理得,BD= ![]() =2
=2 ![]() ,
,
∴OB= ![]() BD=
BD= ![]() ,
,
由折叠得,∠BON=90°,ON= ![]() MN,BN=DN,
MN,BN=DN,
∵BC=BN+CN=4,
∴CN=4﹣BN,
在Rt△CDN中,CD=2,
根据勾股定理得,CN2+CD2=DN2,
(4﹣BN)2+22=BN2,
∴BN= ![]() ,
,
在Rt△BON中,ON= ![]() =
= ![]() ,
,
∴MN=2ON= ![]() ,
,
故选B.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】根据几何图形的面积关系可以形象直观地表示多项式的乘法.例如:(2a+b)(a+b)=2a2+3ab+b2可以用图(1)表示
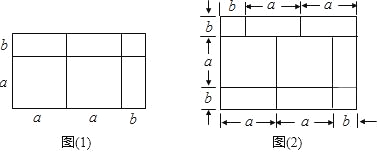
(1)根据图(2),写出一个多项式乘以多项式的等式;
(2)从A,B两题中任选一题作答:
A.请画出一个几何图形,表示(x+p)(x+q)=x2+(p+q)x+pq,并仿照上图标明相应的字母;
B.请画出一个几何图形,表示(x﹣p)(x﹣q)=x2﹣(p+q)x+pq,并仿照上图标明相应的字母.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图象与x轴交于点 A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.
的图象与x轴交于点 A,B,与y轴交于点C.点P是该函数图象上的动点,且位于第一象限,设点P的横坐标为x.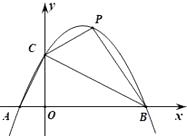
(1)写出线段AC,BC的长度:AC= , BC=;
(2)记△BCP的面积为S,求S关于x的函数表达式;
(3)过点P作PH⊥BC,垂足为H,连结AH,AP,设AP与BC交于点K,探究:是否存在四边形ACPH为平行四边形?若存在,请求出 ![]() 的值;若不存在,请说明理由,并求出
的值;若不存在,请说明理由,并求出 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价8.5折优惠.设顾客预计累计购物![]() 元(
元(![]() ).
).
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)李明准备购买500元的商品,你认为他应该去哪家超市?请说明理由;
(3)计算一下,李明购买多少元的商品时,到两家超市购物所付的费用一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其他项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数 | 频率 |
篮球 | 30 | 0.25 |
羽毛球 | m | 0.20 |
乒乓球 | 36 | n |
跳绳 | 18 | 0.15 |
其他 | 12 | 0.10 |
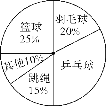
请根据以上图表信息,解答下列问题:
(1)频数分布表中的m=_________,n=_________;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离(结果精确到0.1米,参考数据: ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.
【1】如图1,若点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系PD+PE+PF=AB;当点P在△ABC内,先在图2中作出图形,并写出PD,PE,PF与AB满足的数量关系,然后证明你的结论
【2】当点P在△ABC外,先在图3中作出图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com