
【题目】从邵阳市到长沙的高铁列车里程比普快列车里程缩短了75千米,运行时间减少了4小时,已知邵阳市到长沙的普快列车里程为306千米,高铁列车平均时速是普快列车平均时速的3.5倍.
(1)求高铁列车的平均时速;
(2)某日刘老师从邵阳火车南站到长沙市新大新宾馆参加上午11:00召开的会议,如果他买到当日上午9:20从邵阳市火车站到长沙火车南站的高铁票,而且从长沙火车南站到新大新宾馆最多需要20分钟.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
【答案】
(1)解:设普快的平均时速为x千米/小时,高铁列车的平均时速为3.5x千米/小时,
由题意得, ![]() ﹣
﹣ ![]() =4,
=4,
解得:x=60,
经检验,x=60是原分式方程的解,且符合题意,
则3.5x=210,
答:高铁列车的平均时速为210千米/小时
(2)解:(306﹣75)÷(3.5×60)=1.1小时即66分钟,
66+20=86分钟,
而9:20到11:00相差100分钟,
∵100>86,故在高铁列车准点到达的情况下他能在开会之前赶到
【解析】(1)设普快的平均时速为x千米/小时,高铁列车的平均时速为3.5x千米/小时,根据题意可得,高铁走(306﹣75)千米比普快走306千米时间减少了4小时,据此列方程求解;(2)求出刘老师所用的时间,然后进行判断.
【考点精析】掌握分式方程的应用是解答本题的根本,需要知道列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y= ![]() 的图象上,则k的值为 .
的图象上,则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:n为正整数,点A1(x1 , y1),A2(x2 , y2),A3(x3 , y3),A4(x4 , y4)…An(xn , yn)均在直线y=x﹣1上,点B1(m1 , p1),B2(m2 , p2),B3(m3 , p3)…Bn(mn , pn)均在双曲线y=﹣ ![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为﹣1,则点A2017的坐标为( )
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,A3B3⊥x轴,…,AnBn⊥x轴,BnAn+1⊥y轴,若点A1的横坐标为﹣1,则点A2017的坐标为( ) 
A.(﹣1,﹣2)
B.(2,1)
C.( ![]() ,﹣
,﹣ ![]() )
)
D.( ![]() ,﹣2)
,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1 , 作第1个正方形A1B1C1C;延长C1B1交x轴于点A2 , 作第2个正方形A2B2C2C1 , …,按这样的规律进行下去,第2016个正方形的面积是 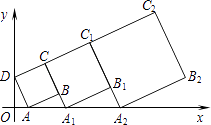
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF. 
(1)求证:直线PA为⊙O的切线;
(2)试探究线段EF、OD、OP之间的等量关系,并加以证明;
(3)若BC=6,tan∠F= ![]() ,求cos∠ACB的值和线段PE的长.
,求cos∠ACB的值和线段PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率;
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)经过点A(1,0),B(3,0),C(0,3).
(1)求抛物线的表达式及顶点D的坐标;
(2)如图甲,点P是直线BC上方抛物线上一动点,过点P作y轴的平行线,交直线BC于点E,是否存在一点P,使线段PE的长最大?若存在,求出PE长的最大值;若不存在,请说明理由;
(3)如图乙,过点A作y轴的平行线,交直线BC于点F,连接DA、DB四边形OAFC沿射线CB方向运动,速度为每秒1个单位长度,运动时间为t秒,当点C与点B重合时立即停止运动,设运动过程中四边形OAFC与四边形ADBF重叠部分面积为S,请求出S与t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com