
【题目】如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( ).
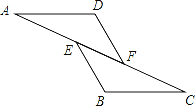
A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC
【答案】B.
【解析】
试题分析:求出AF=CE,再根据全等三角形的判定定理判断即可.∵AE=CF,∴AE+EF=CF+EF,∴AF=CE,A、∵在△ADF和△CBE中,∠A=∠C,AF=CE,∠AFD=∠CEB,∴△ADF≌△CBE(ASA),正确,故本选项错误;B、根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项正确;C、∵在△ADF和△CBE中,AF=CE,∠AFD=∠CEB,DF=BE,∴△ADF≌△CBE(SAS),正确,故本选项错误;D、∵AD∥BC,∴∠A=∠C,∵在△ADF和△CBE中,∠A=∠C,AF=CE,∠AFD=∠CEB,∴△ADF≌△CBE(ASA),正确,故本选项错误.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一次数学检测中,有5名学生的成绩分别是86,89,78,93,90.则这5名学生成绩的平均分和中位数分别是( )
A. 87.2,89 B. 89,89 C. 87.2,78 D. 90,93
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
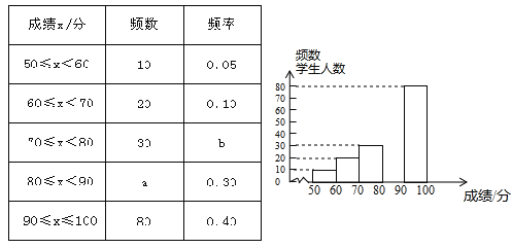
请根据所给信息,解答下列问题:
(1)a=________ , b=________ ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在________ 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有 人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个三角形的两边长分别是3cm和4cm,则第三边长x的取值范围是__________.若x是奇数,则x的值是______;则它的周长为______;若x是偶数,则x的值是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,将点(﹣2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
A.(4,﹣3)
B.(﹣4,3)
C.(0,﹣3)
D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用尺规进行作图,根据下列条件作三角形,画出的三角形不是唯一的是( )
A. 已知三条边
B. 已知三个角
C. 已知两角和夹边
D. 已知两边和夹角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com