
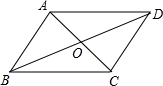
 如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )
如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )| A. | 6 | B. | 2$\sqrt{5}$ | C. | $\sqrt{5}$ | D. | 3 |
分析 根据平行四边形的性质得出AD∥BC,AO=$\frac{1}{2}$AC=1,BD=2BO,求出∠ACB=∠DAC=45°,根据三角形内角和定理求出∠ABC=45°,求出∠ABC=∠ACB,推出AB=AC=2,根据勾股定理求出BO,即可得出答案.
解答 解:∵AB⊥AC,
∴∠BAC=90°,
∵四边形ABCD是平行四边形,AC=2,
∴AD∥BC,AO=$\frac{1}{2}$AC=1,BD=2BO,
∵∠DAC=45°,
∴∠ACB=∠DAC=45°,
∴∠ABC=180°-90°-45°=45°,
∴∠ABC=∠ACB,
∴AB=AC=2,
由勾股定理得:BO=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴BD=2BO=2$\sqrt{5}$,
故选B.
点评 本题考查了等腰三角形判定,勾股定理,平行线的性质,平行四边形的性质,三角形内角和定理的应用,能综合运用定理进行推理是解此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
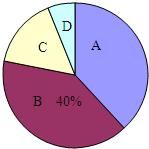 某市共有45000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:
某市共有45000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | 0.38 |
| B | 75~89 | m | x |
| C | 60~74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )| A. | (504,504) | B. | (-504,504) | C. | (-504,-504) | D. | (504,-504) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 相等的两个角是对顶角 | |
| D. | 从直线外一点到这条直线的垂线段,叫做这点到直线的距离 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{2}{5}$ | B. | $-\frac{4}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (1,-1) | C. | (-1,-1) | D. | (-$\frac{1}{2}$,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com