
【题目】在![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 以每秒1个单位的速度从点
以每秒1个单位的速度从点![]() 出发运动到点
出发运动到点![]() ,点
,点![]() 以相同的速度从点
以相同的速度从点![]() 出发运动到点
出发运动到点![]() ,两点同时出发,过点
,两点同时出发,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
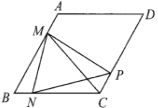
(1)当![]() 和
和![]() 时,请你分别在备用图1,备用图2中画出符合题意的图形;
时,请你分别在备用图1,备用图2中画出符合题意的图形;
(2)当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
(3)当点![]() 在线段
在线段![]() 的延长线上时,是否存在某一时刻
的延长线上时,是否存在某一时刻![]() 使
使![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见解析;(2)当![]() 时,以
时,以![]() 为顶点的四边形是平行四边形 ;(3)
为顶点的四边形是平行四边形 ;(3)![]() 时,
时,![]() .
.
【解析】
(1)根据AM=t![]() 1可得,再根据题意过点过点
1可得,再根据题意过点过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() 即可;
即可;
(2) 过![]() 作
作![]() 于
于![]() ,先证明四边形AMPE是平行四边形,从而得到AM=PE,在Rt△ADE中法求得DE=2,再求出PC=2-t,根据要使以
,先证明四边形AMPE是平行四边形,从而得到AM=PE,在Rt△ADE中法求得DE=2,再求出PC=2-t,根据要使以![]() 为顶点的四边形是平行四边形则AM=PC,得到关于t的方程,解方程即可;
为顶点的四边形是平行四边形则AM=PC,得到关于t的方程,解方程即可;
(3) 当![]() 在线段
在线段![]() 延长线上时,可得
延长线上时,可得![]() ,
,![]() ,
,![]() ,再根据
,再根据![]() 得到关于t的方程,解方程即可.
得到关于t的方程,解方程即可.
(1)如备用图1、2所示;
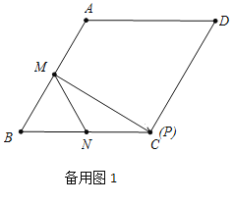
(2)若点![]() 在线段
在线段![]() 上时,过
上时,过![]() 作
作![]() 于
于![]() ,如图
,如图
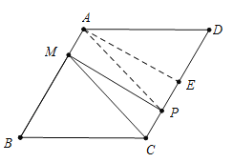
∵![]()
∴![]()
又在平行四边形![]() 中,
中,![]() ,即
,即![]()
∴四边形![]() 是平行四边形 ,
是平行四边形 ,
∴![]()
由运动可知![]()
∴![]() ,
,
在![]() 中
中
![]()
∴![]() ,
,
![]() ,
,
要使四边形![]() 为平行四边形,则只需
为平行四边形,则只需![]() ,
,
即![]() ,解得,
,解得,![]() ,
,
当![]() 时,以
时,以![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
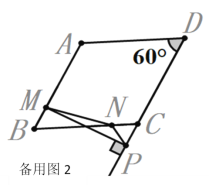
(3)当![]() 在线段
在线段![]() 延长线上时,假设时,如图
延长线上时,假设时,如图
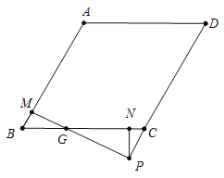
易知![]() ,
,
![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
故![]() 时,
时,![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校课外兴趣小组在本校学生中开展“感动中国2013年度人物”先进事迹知晓情况专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,划分类别后的数据整理如下表:
类别 | A | B | C | D |
频数 | 30 | 40 | 24 | b |
频率 | a | 0.4 | 0.24 | 0.06 |
(1)表中的a= ,b= ;
(2)根据表中数据,求扇形统计图中类别为B的学生数所对应的扇形圆心角的度数;
(3)若该校有学生1000名,根据调查结果估计该校学生中类别为C的人数约为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4. 
(1)求证: ![]() ~△ADB;
~△ADB;
(2) 求![]() 的值;
的值;
(3)延长BC至F,连接FD,使![]() 的面积等于
的面积等于![]() ,求证:DF与⊙O相切。
,求证:DF与⊙O相切。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料1新规定:求若干个相同的有理数(均不等于![]() )的除法运算叫做除方,如
)的除法运算叫做除方,如![]() ,
,![]() 等.类比有理数的乘方,我们把
等.类比有理数的乘方,我们把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”,
次方”,![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”,一般地,把
次方”,一般地,把![]() 记作
记作![]() ,读作“
,读作“![]() 的圈
的圈![]() 次方”.我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
次方”.我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
如: 
(1)直接写出计算结果:  .
.
材料2 新规定:自然数1到![]() 的连乘积用表示
的连乘积用表示![]() ,例如:
,例如:![]() ,
,![]() ,
,![]() ,
,![]() ,……在这种规定下:
,……在这种规定下:
(2)仿照上面的算式,将一个非零有理数![]() 的圈
的圈![]() 次方写成幂的形式等于 ;
次方写成幂的形式等于 ;
(3)一算:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点的坐标分别为A(﹣2,3)、B(﹣6,0)、C(﹣1,0).
(1)画出△ABC关于原点成中心对称的三角形△A′B′C′;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点B″的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民选购家用净水器.我市飞龙商场抓住商机,从厂家购进了A、B两种型号家用净水器共100台,A型号家用净水器进价是150元/台,B型号家用净水器进价是250元/台,购进两种型号的家用净水器共用去19000 元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这100台家用净水器的毛利润不低于5600元,求每台A型号家用净水器的售价至少是多少元? (注: 毛利润=售价一进价) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用300元购进笔记本若干,第二次又用300元购进该款笔记本,但这次每本的进价是第一次进价的![]() 倍,购进数量比第一次少了25本.
倍,购进数量比第一次少了25本.
(1)求第一次每本笔记本的进价是多少元?
(2)若要求这两次购进的笔记本按同一价格全部销售完毕后获利不低于450元,问每本笔记本的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试根据图中信息,解答下列问题.
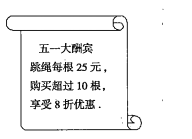
(1)一次性购买6根跳绳需_____元,一次性购买12根跳绳需______元;
(2)小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知,抛物线![]() (a
(a![]() 0)的顶点为A(s,t)(其中s
0)的顶点为A(s,t)(其中s![]() 0) .
0) .
(1)若抛物线经过(2,2)和(-3,37)两点,且s=3.
①求抛物线的解析式;
②若n>3, 设点M(![]() ),N(
),N(![]() )在抛物线上,比较
)在抛物线上,比较![]() ,
,![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)若a=2,c=-2,直线![]() 与抛物线
与抛物线![]() 的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
(3)若点A在抛物线![]() 上,且2≤s<3时,求a的取值范围.
上,且2≤s<3时,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com