
【题目】知,抛物线![]() (a
(a![]() 0)的顶点为A(s,t)(其中s
0)的顶点为A(s,t)(其中s![]() 0) .
0) .
(1)若抛物线经过(2,2)和(-3,37)两点,且s=3.
①求抛物线的解析式;
②若n>3, 设点M(![]() ),N(
),N(![]() )在抛物线上,比较
)在抛物线上,比较![]() ,
,![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)若a=2,c=-2,直线![]() 与抛物线
与抛物线![]() 的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
(3)若点A在抛物线![]() 上,且2≤s<3时,求a的取值范围.
上,且2≤s<3时,求a的取值范围.
【答案】(1)①![]() ②
②![]() (2)
(2)![]() (3)
(3) ![]()
【解析】分析:(1)、首先设抛物线为顶点式,然后利用待定系数法求出函数解析式;利用做差法得出函数的大小关系;(2)、首先分别得出点P和点Q的纵坐标以及两点的差,然后根据两点在抛物线上,从而得出b和h的函数关系式;(3)、设抛物线![]() ,根据经过点C得出一个式子,根据点A在抛物线上得出第二个式子,然后根据S的取值范围得出a的取值范围.
,根据经过点C得出一个式子,根据点A在抛物线上得出第二个式子,然后根据S的取值范围得出a的取值范围.
详解:(1)、①设抛物线的解析式为:![]() ,根据题意得:
,根据题意得:![]() ,
,
解得:![]() . ∴
. ∴![]() .
.
②∵![]() 在抛物线上,∴
在抛物线上,∴![]() . ∴
. ∴![]() . ∵
. ∵![]() , ∴
, ∴![]() .
.
(2)根据题意得:![]() , ∴
, ∴![]() .
.
又∵![]() 在抛物线上, ∴
在抛物线上, ∴![]() . ∴
. ∴![]() .
.
(3)、设抛物线![]() .
.
∵抛物线经过点(0,c),∴![]() ,即:
,即:![]() . ①
. ①
又∵点A在抛物线![]() 上,∴
上,∴![]() ,即:
,即:![]() .②
.②
由①②可得:![]() . ∵
. ∵![]() , ∴
, ∴![]() . ∵
. ∵![]() ,∴
,∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 以每秒1个单位的速度从点
以每秒1个单位的速度从点![]() 出发运动到点
出发运动到点![]() ,点
,点![]() 以相同的速度从点
以相同的速度从点![]() 出发运动到点
出发运动到点![]() ,两点同时出发,过点
,两点同时出发,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
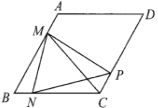
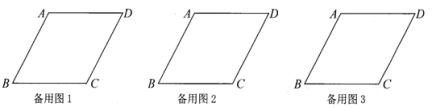
(1)当![]() 和
和![]() 时,请你分别在备用图1,备用图2中画出符合题意的图形;
时,请你分别在备用图1,备用图2中画出符合题意的图形;
(2)当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形;
为顶点的四边形是平行四边形;
(3)当点![]() 在线段
在线段![]() 的延长线上时,是否存在某一时刻
的延长线上时,是否存在某一时刻![]() 使
使![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:
(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的![]() ;
;
(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 A,B,C,D 依次在同一条直线上,点 E,F 分别在直线 AD 的两侧,已知 BE//CF,∠A=∠D,AE=DF.
(1)求证:四边形 BFCE 是平行四边形.
(2)若 AD=10,EC=3,∠EBD=60°,当四边形 BFCE是菱形时,求 AB 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,点C在直线AB上,D为线段BC的中点.
(1)若AB=8 ,AC=2,求线段CD的长.
![]()
(2)若点E是线段AC的中点,直接写出线段DE和AB的数量关系是________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市有三个景区是人们节假日游玩的热点景区,某学校对七(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了如下不完全的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)九(1)班现有学生__________人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________;
(2)请将条形统计图补充完整;
(3)若该校七年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:

(1)九(1)班的学生人数为40,并把条形统计图补充完整;
(2)扇形统计图中m=10,n=20,表示“足球”的扇形的圆心角是72度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A点表示的数是﹣2,B点表示的数是5,C点表示的数是10.
![]()
(1)若要使A、C两点所表示的数是一对相反数,则“原点”表示的数是: .
(2)若此时恰有一只老鼠在B点,一只小猫在C点,老鼠发现小猫后立即以每秒一个单位的速度向点A方向逃跑,小猫随即以每秒两个单位的速度追击.
①在小猫未抓住老鼠前,用时间t(秒)的代数式表示老鼠和小猫在移动过程中分别与点A之间的距离;
②小猫逮住老鼠时的“位置”恰好在 ,求时间t.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com