练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．一个直角三角形的两条直角边长是方程x2-7x+12=0的两个根，则此直角三角形的内切圆的半径为1．

    分析 先解一元二次方程，根据勾股定理解得三角形的斜边，利用直角三角形内切圆的半径等于两直角边之和与斜边之差的一半，可得结果．

    解答 解：解方程x2-7x+12=0得，
    x1=3，x2=4，
    由勾股定理得，斜边为5，
    ∴此直角三角形的内切圆的半径为=$\frac{1}{2}×（3+4-5）$=1，
    故答案为：1．

    点评 本题主要考查了因式分解法解一元二次方程，熟记直角三角形内切圆的半径等于两直角边之和与斜边之差的一半是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．平行四边形不一定具有的特征是（　　）
    A．两组对边分别平行B．两组对角分别相等
    C．对角线相等D．内角和为360°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

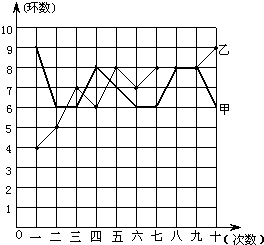    17．射击集训队在在一个月的集训中，对甲、乙两名运动员进行了10次测试，成绩如图所示（折线图中，粗线表示甲，细线表示乙）：
    （1）根据如图所提供的信息填写表格；
    平均数极差方差
    甲731.2
    乙752.2
    （2）如果你是教练，会选择哪位运动员参加比赛？请结合表中三个统计指标以及折线统计图说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．下列说法正确的是（　　）
    A．有公共顶点的两个角是对顶角B．相等的角是对顶角
    C．有公共顶点且相等的角是对顶角D．对顶角相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知：一条抛物线的开口向上，顶点为A（-2，0），与y轴相交于点B，过点B作BC∥x，交抛物线于点C，过点C作CD∥AB，交x轴于点D
    （1）求点D的坐标；
    （2）试探索：AB与BD是否互相垂直？若果能，请求出以这条抛物线为图象的二次函数的解析式；如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．不等式组$\left\{\begin{array}{l}{\frac{1-2x}{4}＜1}\\{x+1≤2}\end{array}\right.$的整数解是-1，0，1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．已知双曲线y=$\frac{a}{x}$与直线y=kx在第一象限的交点为A （3，5），则双曲线y=$\frac{a}{x}$与直线y=kx另一个交点B的坐标为（　　）
    A．（-3，5）B．（3，-5）C．（-5，-3）D．（-3，-5）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

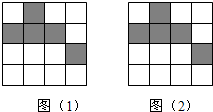    15．如图（1）、（2）分别是由16个小正方形组成的正方形网格图，现已将其中部分小正方形涂黑，请你用两种不同的方法，分别在两个图中再涂黑两个空白的小正方形，使它（涂黑部分）成为轴对称图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图，已知函数y1=3x+b和y2=ax-3的图象交于点P（-2，-5），则不等式3x+b＞ax-3的解集为x＞-2．

    查看答案和解析>>

    同步练习册答案