【题目】如图1，在
中，
，
，
与
相交于点
，且
，
，垂足分别为点
、
.
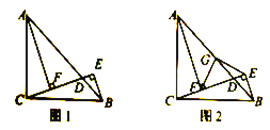
（1）若
，
，求
的长.
（2）如图2，取中点
，连接
、
，请判断
的形状，并说明理由.
【答案】（1）3；（2）
为等腰直角三角形
【解析】
（1）根据AAS只要证明△ACF≌△CBE，得到CE=AF=5，CF=BE=2，即可得到EF；
（2）连接CG，由（1）得到△ABC是等腰直角三角形，CG是中线，得到∠CBG=45°，得到CG=BG，易得到∠GCF=∠GBE，CF=BF，由SAS证明△CFG≌△BEG，得到FG=EG，∠CGF=∠BGE，再由等角互换得到∠FGE=∠AGC=90°，即可得到的形状为等腰直角三角形.
解：（1）∵
∴
∵
∴
∴
∴
∵
，∴
在
和△
中
∴
∴
∵
∴
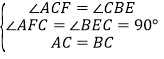
（2）为等腰直角三角形
理由如下：连接
∵
∴
，
∴
∴
∴
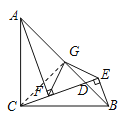
在
和
中
∵
，
∴
由（1）证可知：
∴
∵
∴
∴
∵
∴
∴
∵
∴
即
∴
是等腰直角三角形
科目：初中数学 来源： 题型：
【题目】已知直线CD⊥AB于点O，∠EOF＝90°，射线OP平分∠COF．
（1）如图1，∠EOF在直线CD的右侧：
①若∠COE＝30°，求∠BOF和∠POE的度数；
②请判断∠POE与∠BOP之间存在怎样的数量关系？并说明理由．
（2）如图2，∠EOF在直线CD的左侧，且点E在点F的下方：
①请直接写出∠POE与∠BOP之间的数量关系；
②请直接写出∠POE与∠DOP之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，抛物线y= x2+bx+c与x轴、y轴分别相交于点A（ 1，0）、B（0，3）两点，其顶点为D．
（1）求这条抛物线的解析式；
（2）若抛物线与x轴的另一个交点为E． 求△ODE的面积；抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标，若不存在说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点
、
、
分别在
、
、
上，且
，
，下面写出了说明“
”的过程，请填空：
∵，
∴
_______，
________.（________________________）
∵
∴
___________，（________________________）
∵
∴
___________，（________________________）
∴
.（等量代换）
∵
（平角定义）
∴（等量代换）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平行四边形ABCD中，点A1，A2，A3，A4和C1，C2，C3，C4分别是AB和CD的五等分点，点B1，B2和D1，D2分别是BC和DA的三等分点，已知四边形A4B2C4D2的面积为1cm2，则平行四边形ABCD的面积为（ ）cm2．
A.
B.
C.
D.15
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在ABCD中，M、N分别是AD，BC的中点，∠AND=90°，连接CM交DN于点O．
（1）求证：△ABN≌△CDM；
（2）过点C作CE⊥MN于点E，交DN于点P，若PE=1，∠1=∠2，求AN的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本小题满分8分）某厂制作甲、乙两种环保包装盒。已知同样用6m的材料制成甲盒的个数比制成乙盒的个数少2个，且制成一个甲盒比制作一个乙盒需要多用20%的材料。
（1）求制作每个甲盒、乙盒各用多少材料？
（2）如果制作甲、乙两种包装盒3000个，且甲盒的数量不少于乙盒数量的2倍，那么请写出所需材料总长度
与甲盒数量
之间的函数关系式，并求出最少需要多少米材料。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，CE是平行四边形ABCD的边AB的垂直平分线，垂足为点O，CE与DA的延长线交于点E，连接AC，BE，则下列结论：①AC=AD；②AO=
；③四边形ACBE是菱形；④
．其中正确的结论有____．(填写所有正确结论的序号)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，D是BC边上的点（不与点B，C重合），连结AD
（1）如图1,当点D是BC边上的中点时，则S△ABD:S△ACD=_________（直接写出答案）
（2）如图2，当AD是∠BAC的平分线时，若AB=m，AC=n，S△ABD:S△ACD=_________ (用含m,n的代数式表示)．
（3）如图3，AD平分∠BAC，延长AD到E，使得AD=DE,连结BE，如果AC=2,AB=4,S△BDE =6,求△ABC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com