
���� ��1�����Ȼ���״ͼչʾ����16�ֵȿ��ܵĽ��������������������С���ŵĺ͵���4��ռ3�֣�Ȼ����ݸ��ʵĸ�����㼴�ɣ�
���ɢٿ�֪��16�ֵȿ��ܵĽ���������е�һ��ȡ����С�����ܱ��ڶ���ȡ����С������������8�֣��������������ʣ�
��2�����������г���Ӧ�ı��ó����еȿ��ܵ���������ҳ�����ȡ����С��ı�ŵĺ͵���4��������������������ĸ��ʣ�
��� �⣺��1������ͼ��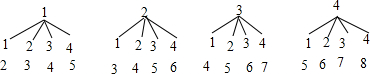
���������һ��С��Ȼ��Żأ������������һ��С����16�ֵȿ��ܵĽ��������������������С���ŵĺ͵���4��ռ3�֣�
��������������С���ŵĺ͵���4�ĸ���$\frac{3}{16}$��
�����е�һ��ȡ����С�����ܱ��ڶ���ȡ����С������������8�֣����������=$\frac{8}{16}$=$\frac{1}{2}$��
��2���б��ã�
| 1 | 2 | 3 | 4 | |
| 1 | --- | ��2��1�� | ��3��1�� | ��4��1�� |
| 2 | ��1��2�� | --- | ��3��2�� | ��4��2�� |
| 3 | ��1��3�� | ��2��3�� | --- | ��4��3�� |
| 4 | ��1��4�� | ��2��4�� | ��3��4�� | --- |
���� ���⿼��������б�������״ͼ������ʣ��б������Բ��ظ�����©���г����п��ܵĽ�����ʺ���������ɵ��¼�����״ͼ���ʺ�����������������ɵ��¼�������ʱҪע������ǷŻ�ʵ�黹�Dz��Ż�ʵ�飮�õ���֪ʶ��Ϊ������=������������������֮�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2-y | B�� | x2+1 | C�� | x2-6x | D�� | x2+y+y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
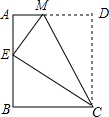 ��ͼ��������ABCD��CM�۵���ʹ��D����AB���ϵĵ�E����
��ͼ��������ABCD��CM�۵���ʹ��D����AB���ϵĵ�E�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
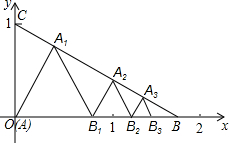 ��ͼ��ʾ����֪�ڡ�ABC�У�A��0��0����B��$\sqrt{3}$��0����C��0��1�����ڡ�ABC���������ȱ������Σ������ĵȱ������ηֱ��ǵ�1����AA1B1����2����B1A2B2����3����B2A3B3������ʹB1��B2��B3������x���ϣ�A1��A2��A3������BC���ϣ����n���ȱ������εı߳����ڣ�������
��ͼ��ʾ����֪�ڡ�ABC�У�A��0��0����B��$\sqrt{3}$��0����C��0��1�����ڡ�ABC���������ȱ������Σ������ĵȱ������ηֱ��ǵ�1����AA1B1����2����B1A2B2����3����B2A3B3������ʹB1��B2��B3������x���ϣ�A1��A2��A3������BC���ϣ����n���ȱ������εı߳����ڣ�������| A�� | $\frac{\sqrt{3}}{{2}^{n}}$ | B�� | $\frac{\sqrt{3}}{{2}^{n-1}}$ | C�� | $\frac{3}{{2}^{n}}$ | D�� | $\frac{3}{{2}^{n-1}}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
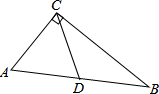 ��ͼ����Rt��ABC�У���ACB=90�㣬D��AB���е㣬��AB=16����CD�ij��ǣ�������
��ͼ����Rt��ABC�У���ACB=90�㣬D��AB���е㣬��AB=16����CD�ij��ǣ�������| A�� | 6 | B�� | 8 | C�� | 10 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
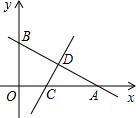 ��ͼ��һ�κ���y=-$\frac{2}{3}$x+b��ͼ����x�ᡢy��ֱ��ڵ�A��B���߶�AB���е�ΪD��3��2��������AOB��ֱ��CD�۵���ʹ��A���B�غϣ�ֱ��CD��x�ύ�ڵ�C��
��ͼ��һ�κ���y=-$\frac{2}{3}$x+b��ͼ����x�ᡢy��ֱ��ڵ�A��B���߶�AB���е�ΪD��3��2��������AOB��ֱ��CD�۵���ʹ��A���B�غϣ�ֱ��CD��x�ύ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����������У�����ʼ�����xֵΪ24�����Ƿ��ֵ�1������Ľ��Ϊ 12����2������Ľ��Ϊ6������2012������Ľ��Ϊ6��
��ͼ��ʾ����������У�����ʼ�����xֵΪ24�����Ƿ��ֵ�1������Ľ��Ϊ 12����2������Ľ��Ϊ6������2012������Ľ��Ϊ6���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com