
ЎѕМвДїЎїДіКРОЄБЛЅЁЙи№ъјТј¶ОАЙъіЗКР.КРХюІїГЕѕц¶ЁґоЕдAЎўBБЅЦЦФ°ТХФмРН№І50ёц°Ъ·ЕФЪКРЗшЈ¬ПЦУР3490ЕијЧЦЦ»Ё»ЬєН2950ЕиТТЦЦ»Ё»ЬїЙ№©К№УГЈ¬ТСЦЄґоЕдТ»ёцAЦЦФмРНРијЧЦЦ»Ё»Ь80ЕиЈ¬ТТЦЦ»Ё»Ь40ЕиЈ¬ґоЕдТ»ёцBЦЦФмРНРијЧЦЦ»Ё»Ь50ЕиЈ¬ТТЦЦ»Ё»Ь90Еи.
ЈЁ1Ј©ОК·ыєПМвТвµДґоЕд·Ѕ°ёУРјёЦЦЈїЗлДг°пЦъЙијЖіцАґ.
ЈЁ2Ј©ИфґоЕдТ»ёцAЦЦФмРНµД·СУГКЗ800ФЄЈ¬ґоЕдТ»ёцBЦЦФмРНµД·СУГКЗ960ФЄЈ¬КФЛµГчЈЁ1Ј©ЦРДДЦЦ·Ѕ°ё·СУГЧоµНЈїЧоµН·СУГКЗ¶аЙЩФЄЈї
Ўѕґр°ёЎїЈЁ1Ј©·Ѕ°ёТ»Јє31ёцAЎў19ёцBЈ¬·Ѕ°ё¶юЈє32ёцAЎў18ёцBЈ¬·Ѕ°ёИэЈє33ёцAЎў17ёцBЈ»ЈЁ2Ј©42720ФЄ
ЎѕЅвОцЎї
ЈЁ1Ј©°Ъ·Е50ёцФ°ТХФмРНЛщРиµДјЧЦЦєНТТЦЦ»Ё»ЬУ¦ЈјПЦУРµДЕиКэЈ¬їЙУЙґЛБРіцІ»µИКЅЗуіц·ыєПМвТвµДґоЕд·Ѕ°ёАґЈ»
ЈЁ2Ј©ёщѕЭБЅЦЦФмРНµҐјЫµДіЙ±ѕ·СїЙ·Ц±рјЖЛгіцёчЦЦїЙРР·Ѕ°ёЛщРиµДіЙ±ѕЈ¬И»єуЅшРР±ИЅПЈ»ТІїЙУЙБЅЦЦФмРНµДµҐјЫЦЄµҐјЫіЙ±ѕЅПµНµДФмРНЅП¶а¶шµҐјЫіЙ±ѕЅПёЯµДФмРНЅПЙЩЈ¬ЛщРиµДЧЬіЙ±ѕѕНµНЈ®
ЅвЈєЈЁ1Ј©ЙиґоЕдAЦЦФмРНxёцЈ¬ФтBЦЦФмРНОЄЈЁ50©ЃxЈ©ёцЈ¬ёщѕЭМвТв
![]() Ј¬
Ј¬
ЅвЦ®µГЈє![]()
ЎЯxКЗХыКэЈ¬
ЎаxїЙИЎ31Ј¬32Ј¬33
ЎаїЙЙијЖИэЦЦґоЕд·Ѕ°ёЈ¬·Ц±рОЄЈє
·Ѕ°ёТ»Јє31ёцAЈ¬19ёцBЈ»
·Ѕ°ё¶юЈє32ёцAЈ¬18ёцBЈ»
·Ѕ°ёИэЈє33ёцAЈ¬17ёцBЈ®
ЈЁ2Ј©Из№ыТ»ёцAФмРН·СУГ800ФЄЈ¬Т»ёцBФмРН·СУГ960ФЄЈ¬Фтёчёц·Ѕ°ё·СУГ·Ц±рОЄЈє
·Ѕ°ёТ»Ј¬31ЎБ800+19ЎБ960=43040ФЄ
·Ѕ°ё¶юЈ¬32ЎБ800+18ЎБ960=42880ФЄ
·Ѕ°ёИэЈ¬33ЎБ800+17ЎБ960=42720ФЄ
НЁ№эЙПКцјЖЛг·ўПЦЈ¬·Ѕ°ёИэ·СУГЧоµНЈ¬ЧоµНОЄ42720ФЄ


 АшФЕКйТµКојЩПОЅУДюІЁіц°жЙзПµБРґр°ё
АшФЕКйТµКојЩПОЅУДюІЁіц°жЙзПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬µИСьИэЅЗРОЎчABCµДСьі¤AB=AC=25Ј¬BC=40Ј¬¶ЇµгPґУBіц·ўСШBCПтCФЛ¶ЇЈ¬ЛЩ¶ИОЄ10µҐО»/ГлЈ®¶ЇµгQґУCіц·ўСШCAПтAФЛ¶ЇЈ¬ЛЩ¶ИОЄ5µҐО»/ГлЈ¬µ±Т»ёцµгµЅґпЦХµгµДК±єтБЅёцµгН¬К±НЈЦ№ФЛ¶ЇЈ¬µгPЎдКЗµгP№ШУЪЦ±ПЯACµД¶ФіЖµгЈ¬Б¬ЅУPЎдPєНPЎдQЈ¬ЙиФЛ¶ЇК±јдОЄtГлЈ®
ЈЁ1Ј©Ифµ±tµДЦµОЄmК±Ј¬PPЎдЗЎєГѕ№эµгAЈ¬ЗуmµДЦµЈ®
ЈЁ2Ј©ЙиЎчPЎдPQµДГж»эОЄyЈ¬ЗуyУлtЦ®јдµДєЇКэ№ШПµКЅЈЁmЈјtЎЬ4Ј©
ЈЁ3Ј©КЗ·сґжФЪДіТ»К±їМtЈ¬К№PQЖЅ·ЦЅЗЎПPЎдPCЈїґжФЪЈ¬ЗуПаУ¦µДtЦµЈ¬І»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїДіЦРС§їЄНЁБЛ»ҐБЄНшјТРЈєПУэЅМУэЖЅМЁЈ¬ОЄБЛЅвјТі¤К№УГЖЅМЁµДЗйїцЈ¬С§РЈЅ«јТі¤µДК№УГЗйїц·ЦОЄЎ±ѕіЈК№УГЎ±ЎўЎ°Еј¶ыК№УГЎ±Ў°єНЎ°І»К№УГЎ±ИэЦЦАаРНЈ¬ЅиЦъёГЖЅМЁґуКэѕЭ№¦ДЬЈ¬»гЧЬіцёГРЈ°ЛЈЁ1Ј©°аєН°ЛЈЁ2Ј©°аИ«МејТі¤µДК№УГЗйїцЈ¬Іў»жЦЖіЙИзНјЛщКѕµДБЅ·щІ»НкХыµДНіјЖНјЈє

ЗлёщѕЭНјЦРРЕПўЅвґрПВБРОКМв
ЈЁ1Ј©ґЛґОµчІйµДјТі¤ЧЬИЛКэОЄЎЎ ЎЎЈ»
ЈЁ2Ј©ЙИРОНіјЖНјЦРґъ±нЎ°І»К№УГЎ±АаРНµДЙИРОФІРДЅЗµД¶ИКэКЗЎЎ ЎЎЎгЈ¬ІўІ№И«МхРОНіјЖНјЈ»
ЈЁ3Ј©ИфёГРЈ°ЛДкј¶С§ЙъјТі¤№ІУР1200ИЛЈ¬ёщѕЭґЛґОµчІйЅб№ы№АјЖёГРЈ°ЛДкј¶ЦРЎ°ѕіЈК№УГЎ±АаРНµДјТі¤ФјУР¶аЙЩИЛЈї
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄ¶юґОєЇКэy=ax2+bx+cЈЁaЎЩ0Ј©µДНјПуИзНјЛщКѕЈ¬ПВБРЅбВЫЈєўЩbЈј0Ј»ўЪ4a+2b+cЈј0Ј»ўЫa©Ѓb+cЈѕ0Ј»ўЬЈЁa+cЈ©2Јјb2 Ј® ЖдЦРХэИ·µДЅбВЫКЗЈЁ Ј©
A.ўЩўЪ
B.ўЩўЫ
C.ўЩўЫўЬ
D.ўЩўЪўЫўЬ
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїНкіЙПВБРНЖАнВЫЦ¤№эіМЈє
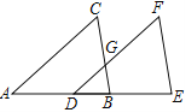
ИзНјЈ¬ТСЦЄЎПAЈЅЎПEDFЈ¬ЎПCЈЅЎПFЈ¬
ЗуЦ¤ЈєBCЎОEF
Ц¤ГчЈєЎЯЎПAЈЅЎПEDFЈЁ Ј©
Ўа________ЎО________ЈЁ Ј©
ЎаЎПCЈЅЎПBGDЈЁ Ј©
УЦЎЯЎПCЈЅЎПF ЈЁ ТСЦЄ Ј©
Ўа_______ЈЅЎПFЈЁµИБїґъ»» Ј©
ЎаBCЎОEFЈЁ Ј©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїёщѕЭФД¶БДЪИЭЈ¬ФЪАЁєЕДЪМоРґНЖАнТАѕЭЈ®
Из№ыБЅМхЖЅРРПЯ±»ИэМхЦ±ПЯЛщЅШЈ¬ДЗГґТ»¶ФДЪґнЅЗµДЅЗЖЅ·ЦПЯТ»¶Ё»ҐПаЖЅРРЈ®
ТСЦЄЈєABЎОCDЈ¬EMЖЅ·ЦЎПAEFЈ¬FNЖЅ·ЦЎПEFD
ЗуЦ¤Јє EMЎОFN

Ц¤ГчЈє
ЎЯABЎОCD
ЎаЎПAEF=ЎПDFE ЈЁ Ј©
ЎЯEMЖЅ·ЦЎПAEF
ЎаЎПMEF=![]() ЎП AEF ЈЁ Ј©
ЎП AEF ЈЁ Ј©
ЎЯFNЖЅ·ЦЎПEFD
ЎаЎПEFN=![]() ЎП EFD ЈЁ Ј©
ЎП EFD ЈЁ Ј©
ЎаЎПMEF=ЎП EFN
Ўа EM ЎОFN ЈЁ Ј©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїТСЦЄЈєИзНјЈ¬ФЪЎчABCЦРЈ¬BC=ACЈ¬ТФBCОЄЦ±ѕ¶µДЎСOУл±ЯABПаЅ»УЪµгDЈ¬DEЎНACЈ¬ґ№ЧгОЄµгEЈ®
ЈЁ1Ј©ЗуЦ¤ЈєµгDКЗABµДЦРµгЈ»
ЈЁ2Ј©ЕР¶ПDEУлЎСOµДО»ЦГ№ШПµЈ¬ІўЦ¤ГчДгµДЅбВЫЈ»
ЈЁ3Ј©ИфЎСOµДЦ±ѕ¶ОЄ18Ј¬cosB= ![]() Ј¬ЗуDEµДі¤Ј®
Ј¬ЗуDEµДі¤Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјКЗ¶юґОєЇКэy=ax2+bx+cНјПуµДТ»Ії·ЦЈ¬НјПу№эµгAЈЁ©Ѓ3Ј¬0Ј©Ј¬¶ФіЖЦбОЄЦ±ПЯx=©Ѓ1Ј¬ёшіцЛДёцЅбВЫЈє
ўЩcЈѕ0Ј»
ўЪИфµгBЈЁ©Ѓ ![]() Ј¬y1Ј©ЎўCЈЁ©Ѓ
Ј¬y1Ј©ЎўCЈЁ©Ѓ ![]() Ј¬y2Ј©ОЄєЇКэНјПуЙПµДБЅµгЈ¬Фтy1Јјy2Ј»
Ј¬y2Ј©ОЄєЇКэНјПуЙПµДБЅµгЈ¬Фтy1Јјy2Ј»
ўЫ2a©Ѓb=0Ј»
ўЬ ![]() Јј0Ј¬
Јј0Ј¬
ЖдЦРЈ¬ХэИ·ЅбВЫµДёцКэКЗЈЁ Ј©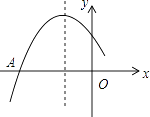
A.1
B.2
C.3
D.4
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФД¶БІДБПЈє°СРОИз![]() µД¶юґОИэПоКЅЈЁ»тЖдТ»Ії·ЦЈ©ЕдіЙНкИ«ЖЅ·ЅКЅµД·Ѕ·ЁЅРЧцЕд·Ѕ·Ё.Ед·Ѕ·ЁµД»щ±ѕРОКЅКЗНкИ«ЖЅ·Ѕ№«КЅµДДжРґЈ¬јґ
µД¶юґОИэПоКЅЈЁ»тЖдТ»Ії·ЦЈ©ЕдіЙНкИ«ЖЅ·ЅКЅµД·Ѕ·ЁЅРЧцЕд·Ѕ·Ё.Ед·Ѕ·ЁµД»щ±ѕРОКЅКЗНкИ«ЖЅ·Ѕ№«КЅµДДжРґЈ¬јґ![]() .АэИзЈє
.АэИзЈє![]()
![]() КЗ
КЗ![]() µДТ»ЦЦРОКЅµДЕд·ЅЈ»ЛщТФЈ¬
µДТ»ЦЦРОКЅµДЕд·ЅЈ»ЛщТФЈ¬![]() Ј¬
Ј¬![]()
![]() Ј¬
Ј¬![]() КЗ
КЗ![]() µДИэЦЦІ»Н¬РОКЅµДЕд·ЅЈЁјґЎ°УаПоЎ±·Ц±рКЗіЈКэПоЎўТ»ґОПоЎў¶юґОПоЈ©.
µДИэЦЦІ»Н¬РОКЅµДЕд·ЅЈЁјґЎ°УаПоЎ±·Ц±рКЗіЈКэПоЎўТ»ґОПоЎў¶юґОПоЈ©.
ЗлёщѕЭФД¶БІДБПЅвѕцПВБРОКМвЈє
ЈЁ1Ј©±ИХХЙПГжµДАэЧУЈ¬Рґіц![]() ИэЦЦІ»Н¬РОКЅµДЕд·ЅЈ»
ИэЦЦІ»Н¬РОКЅµДЕд·ЅЈ»
ЈЁ2Ј©ТСЦЄ![]() Ј¬Зу
Ј¬Зу![]() µДЦµЈ»
µДЦµЈ»
ЈЁ3Ј©ТСЦЄ![]() Ј¬Зу
Ј¬Зу![]() µДЦµ.
µДЦµ.
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com