
����Ŀ����ͼ�����������Ρ�ABC������AB=AC=25��BC=40������P��B������BC��C�˶����ٶ�Ϊ10��λ/�룮����Q��C������CA��A�˶����ٶ�Ϊ5��λ/�룬��һ���㵽���յ��ʱ��������ͬʱֹͣ�˶�����P���ǵ�P����ֱ��AC�ĶԳƵ㣬����P��P��P��Q�����˶�ʱ��Ϊt�룮
��1������t��ֵΪmʱ��PP��ǡ�þ�����A����m��ֵ��
��2�����P��PQ�����Ϊy����y��t֮��ĺ�����ϵʽ��m��t��4��
��3���Ƿ����ijһʱ��t��ʹPQƽ�ֽǡ�P��PC�����ڣ�����Ӧ��tֵ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺��ͼ1�У���AM��BC��M��
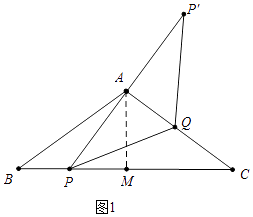
��AB=AC=25��AM��BC��
��BM=MC=20��
��Rt��ABM��AM= ![]() =
= ![]() =15��
=15��
��PP��ǡ�þ�����A����cos��C= ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��t= ![]() ��
��
��m= ![]() s
s
��2���⣺��ͼ2�У���PP�佻AC��N��
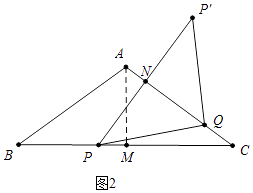
�� ![]() ��t��4ʱ���ɡ�PCN�ס�ACM���ɵ�PC=40��10t��PN=P��N=24��6t��CN=32��8t��
��t��4ʱ���ɡ�PCN�ס�ACM���ɵ�PC=40��10t��PN=P��N=24��6t��CN=32��8t��
��CQ=5t��
��NQ=CN��CQ=32��13t��
��y= ![]() PP��NQ=
PP��NQ= ![]() ��48��12t����32��13t��=78t2��504t+768��
��48��12t����32��13t��=78t2��504t+768�� ![]() ��t��4��
��t��4��
��3���⣺���ڣ��������£�
��ͼ3�У���QE��BC��E��
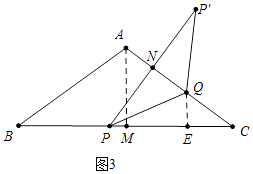
��PQƽ�֡�CPP�䣬QE��PC��QN��PP�䣬
��QN=QE��
��sin��C= ![]() =
= ![]() ��
��![]()
��t=2��
��t=2ʱ��PQƽ�ֽǡ�P��PC
����������1���ɡ�C�����Ҷ������Rt��APC���ֿ���Rt��ACM���г�����ʽ��������ȣ��������̣����m;��2���ɡ�PCN�ס�ACM,�ɱ�ʾ��PC=40��10t��PN=P��N=24��6t,CN=32��8t�����������ʽ�����ɵ�y= ![]() PP��NQ=78t2��504t+768;��3�����á�C�����������ֱ�ʾ�ı���ʽ��������ȣ����г�����,���t.
PP��NQ=78t2��504t+768;��3�����á�C�����������ֱ�ʾ�ı���ʽ��������ȣ����г�����,���t.
�����㾫����������Ҫ���������������ε��ж������ʺ�������Ǻ����Ķ�������֪ʶ�㣬��Ҫ�������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ�������A�����ҡ����ҡ����С����ж�������A��������Ǻ���������ȷ�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Ա�μ����ѵ�����ɼ��ֱ��Ƴ���������ͳ��ͼ��

����������Ϣ�����������������£�
ƽ���ɼ�/�� | ��λ��/�� | ����/�� | ���� | |
�� |
| 7 | 7 | 1.2 |
�� | 7 |
| 8 | 4.2 |
��1���������![]() ��
��![]() ��ֵ��
��ֵ��
��2���ӷ���ĽǶȿ�����ѡ������һ������������ΪӦѡ������Ա����˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��������
��������![]() �������ݿɡ��ѱ䡱�����ɸ����������ĺͣ���
�������ݿɡ��ѱ䡱�����ɸ����������ĺͣ���![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ���ѱ䡱��������һ��������
���ѱ䡱��������һ��������![]() ����
����![]() ��ֵ�ǣ� ��
��ֵ�ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����ѧ��������д����������ǿ�������ֵ���ʶ��ijУ�ٰ����조������д��������ѧ����ѡ�κ������������Է����ǣ���д100�����֣�ÿ��ȷ��д��һ�����ֵ�1�֣����ξ�����ѧ���ɼ�Ϊx���֣�����50��x��100�����䰴�����η�Ϊ���飬���Ƴ����²���������
��� | �ɼ�x���֣� | Ƶ���������� | Ƶ�� |
һ | 50��x��60 | 2 | 0.04 |
�� | 60��x��70 | 10 | 0.2 |
�� | 70��x��80 | 14 | b |
�� | 80��x��90 | a | 0.32 |
�� | 90��x��100 | 8 | 0.16 |
����ݱ����ṩ����Ϣ������������⣺
��1��ֱ��д������a= �� b=��
��2���벹ȫ������Ӧ��Ƶ���ֲ�ֱ��ͼ��
��3���������ɼ�������80��Ϊ���㣬�δ�����������Ϊ ��
��4������ݵõ���ͳ�����ݣ���Ҫ������Щͬѧ�ĺ�����д��������Ϊ���ͬѧ�ǵ���д����������һ�����飨���Ὠ�鲻����20�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ƽ���ı���ABCD���ӳ�AD��E��ʹDE=AD������BE��DC����O�㣮
��1����֤����BOC�ա�EOD��
��2������ABE����ʲô����ʱ���ı���BCED�����Σ�֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У��������ε��ڽ�ƽ�������γɵĽǴ���һ���Ĺ��ɣ����Ⲣ�������еĹ��ɣ�������ͬѧ�ǹ�����ص���ѧ֪ʶ��
��ͼ1��![]() �У�
�У�![]() �ֱ�ƽ��
�ֱ�ƽ��![]() �����ཻ�ڵ�
�����ཻ�ڵ�![]() ���ڷ�С������ͬѧ����:
���ڷ�С������ͬѧ����:![]() ��֤����������:
��֤����������:

֤��:��ͼ2������![]() ���ӳ���
���ӳ���

��![]() (����1)
(����1)
![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]()
![]()
![]()
![]()
![]()
![]()
��![]() ��(����2)
��(����2)
![]() ��
��
![]() ����1�� ___������2�� __��
����1�� ___������2�� __��
![]() ��ͼ3����ͼ1�Ļ����ϣ���
��ͼ3����ͼ1�Ļ����ϣ���![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ���ڵ�
���ڵ�![]() ��̽��
��̽��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������κ���ͼ��Ķ��㡢���ڷ�����ͬ��������������κ���Ϊ��ͬ�ض��κ�����
��1����ֱ��д������Ϊ��ͬ�ض��κ������ĺ�������______����_________��
��2����֪����![]() �Ķ��κ���
�Ķ��κ���![]() ��
��![]() ����
����![]() ��
��![]() Ϊ��ͬ�ض��κ�����������
Ϊ��ͬ�ض��κ�����������![]() �ı���ʽ���������
�ı���ʽ���������![]() ʱ��
ʱ��![]() ����Сֵ��
����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪�����߾���A����4��0����B��0����4����C��2��0�����㣮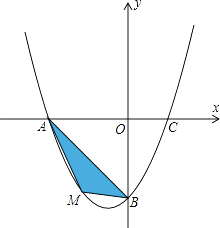
��1���������ߵĽ���ʽ��
��2������MΪ������������������һ���㣬��M�ĺ�����Ϊm����AMB�����ΪS��
��S����m�ĺ�����ϵʽ�������S�����ֵ��
��3������P���������ϵĶ��㣬��Q��ֱ��y=��x�ϵĶ��㣬�ж��м���λ���ܹ�ʹ�õ�P��Q��B��OΪ������ı���Ϊƽ���ı��Σ�ֱ��д����Ӧ�ĵ�Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽�����Ҽ���������.�������ž�������A��B����������50���ڷ�������������3490����ֻ��ܺ�2950�����ֻ��ܿɹ�ʹ�ã���֪����һ��A����������ֻ���80�裬���ֻ���40�裬����һ��B����������ֻ���50�裬���ֻ���90��.
��1���ʷ�������Ĵ��䷽���м��֣����������Ƴ���.
��2��������һ��A�����͵ķ�����800Ԫ������һ��B�����͵ķ�����960Ԫ����˵����1�������ַ���������ͣ���ͷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com