
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.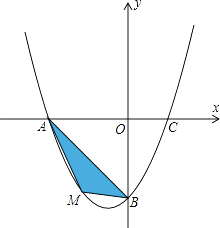
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
【答案】
(1)解:设此抛物线的函数解析式为:
y=ax2+bx+c(a≠0),
将A(﹣4,0),B(0,﹣4),C(2,0)三点代入函数解析式得:
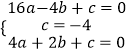
解得 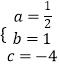 ,
,
所以此函数解析式为:y= ![]()
(2)解:∵M点的横坐标为m,且点M在这条抛物线上,
∴M点的坐标为:(m, ![]() ),
),
∴S=S△AOM+S△OBM﹣S△AOB
= ![]() ×4×(﹣
×4×(﹣ ![]() m2﹣m+4)+
m2﹣m+4)+ ![]() ×4×(﹣m)﹣
×4×(﹣m)﹣ ![]() ×4×4
×4×4
=﹣m2﹣2m+8﹣2m﹣8
=﹣m2﹣4m,
=﹣(m+2)2+4,
∵﹣4<m<0,
当m=﹣2时,S有最大值为:S=﹣4+8=4.
答:m=﹣2时S有最大值S=4
(3)解:设P(x, ![]() x2+x﹣4).
x2+x﹣4).
当OB为边时,根据平行四边形的性质知PQ∥OB,且PQ=OB,
∴Q的横坐标等于P的横坐标,
又∵直线的解析式为y=﹣x,
则Q(x,﹣x).
由PQ=OB,得|﹣x﹣( ![]() x2+x﹣4)|=4,
x2+x﹣4)|=4,
解得x=0,﹣4,﹣2±2 ![]() .
.
x=0不合题意,舍去.
如图,当BO为对角线时,知A与P应该重合,OP=4.四边形PBQO为平行四边形则BQ=OP=4,Q横坐标为4,代入y=﹣x得出Q为(4,﹣4).
由此可得Q(﹣4,4)或(﹣2+2 ![]() ,2﹣2
,2﹣2 ![]() )或(﹣2﹣2
)或(﹣2﹣2 ![]() ,2+2
,2+2 ![]() )或(4,﹣4).
)或(4,﹣4).

【解析】(1)利用待定系数法,把ABC三点坐标代入解析式即可求出;(2)最值问题的基本解决策略就是函数思想,设出M的横坐标为m,作为自变量,△AMB的面积为S为函数,由已知得S=S△AOM+S△OBM﹣S△AOB,分别用m的代数式表示各三角形面积,构建出二次函数,运用配方法求出最大值;(3)可分类讨论:OB为边,根据平行四边形的性质知PQ∥OB,且PQ=OB,构建方程|﹣x﹣( 1 2 x2+x﹣4)|=4;当BO为对角线时,A与P应该重合,OP=4.四边形PBQO为平行四边形,则BQ=OP=4,进而求出坐标.


科目:初中数学 来源: 题型:
【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形△ABC的腰长AB=AC=25,BC=40,动点P从B出发沿BC向C运动,速度为10单位/秒.动点Q从C出发沿CA向A运动,速度为5单位/秒,当一个点到达终点的时候两个点同时停止运动,点P′是点P关于直线AC的对称点,连接P′P和P′Q,设运动时间为t秒.
(1)若当t的值为m时,PP′恰好经过点A,求m的值.
(2)设△P′PQ的面积为y,求y与t之间的函数关系式(m<t≤4)
(3)是否存在某一时刻t,使PQ平分角∠P′PC?存在,求相应的t值,不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
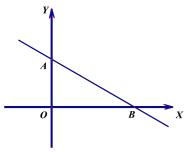
【题目】如图,直线![]() 图像与y轴、x轴分别交于A、B两点
图像与y轴、x轴分别交于A、B两点
(1)求点A、B坐标和∠BAO度数
(2)点C、D分别是线段OA、AB上一动点(不与端点重合),且CD=DA,设线段OC的长度为x ,![]() ,请求出y关于x的函数关系式以及定义域
,请求出y关于x的函数关系式以及定义域
(3)点C、D分别是射线OA、射线BA上一动点,且CD=DA,当ΔODB为等腰三角形时,求C的坐标(第(3)小题直接写出分类情况和答案,不用过程)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,动点
的中点,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 的速度沿
的速度沿![]() 运动,最终到达点
运动,最终到达点![]() .若点
.若点![]() 运动的时间为
运动的时间为![]() 秒,那么当
秒,那么当![]() _____________秒时,
_____________秒时,![]() 的面积等于
的面积等于![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开通了互联网家校合育教育平台,为了解家长使用平台的情况,学校将家长的使用情况分为”经常使用”、“偶尔使用”“和“不使用”三种类型,借助该平台大数据功能,汇总出该校八(1)班和八(2)班全体家长的使用情况,并绘制成如图所示的两幅不完整的统计图:

请根据图中信息解答下列问题
(1)此次调查的家长总人数为 ;
(2)扇形统计图中代表“不使用”类型的扇形圆心角的度数是 °,并补全条形统计图;
(3)若该校八年级学生家长共有1200人,根据此次调查结果估计该校八年级中“经常使用”类型的家长约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②4a+2b+c<0;③a﹣b+c>0;④(a+c)2<b2 . 其中正确的结论是( )
A.①②
B.①③
C.①③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出四个结论:
①c>0;
②若点B(﹣ ![]() ,y1)、C(﹣
,y1)、C(﹣ ![]() ,y2)为函数图象上的两点,则y1<y2;
,y2)为函数图象上的两点,则y1<y2;
③2a﹣b=0;
④ ![]() <0,
<0,
其中,正确结论的个数是( )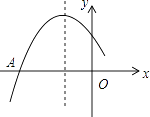
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com