
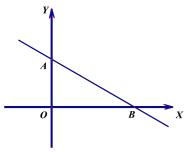
【题目】如图,直线![]() 图像与y轴、x轴分别交于A、B两点
图像与y轴、x轴分别交于A、B两点
(1)求点A、B坐标和∠BAO度数
(2)点C、D分别是线段OA、AB上一动点(不与端点重合),且CD=DA,设线段OC的长度为x ,![]() ,请求出y关于x的函数关系式以及定义域
,请求出y关于x的函数关系式以及定义域
(3)点C、D分别是射线OA、射线BA上一动点,且CD=DA,当ΔODB为等腰三角形时,求C的坐标(第(3)小题直接写出分类情况和答案,不用过程)


【答案】(1)A(0,3),B(![]() ),60°(2)
),60°(2)![]() (0<x<3)(3)(0,0),
(0<x<3)(3)(0,0),![]() ,(0,6)
,(0,6)
【解析】
(1)对于一次函数解析式,分别令x与y为0求出对应的y与x的值,得到A、B两点坐标,然后再根据三角函数求出∠BAO的度数即可;
(2)先证明△ACD是等边三角形,根据等边三角形的性质可得AD=CD=AC=3-x,作DH⊥y轴于点H,用含x的式子表示出DH的长,然后根据三角形面积公式进行求解即可;
(3)当△ODB为等腰三角形时,分三种情况讨论:当OD=DB时;当BD=BO时;当OD=OB时,利用等边三角形的性质分别求出C点坐标即可.
(1)一次函数![]() ,
,
令![]() ,则有
,则有![]() ,解得:
,解得:![]() ,
,![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,
,
![]() ,
,
在![]()
![]() ,
,![]() ,
,
∵sin∠ABO=![]() ,
,
![]() ,
,
![]() ;
;
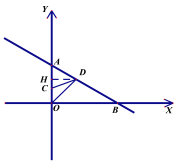
(2)过点D作DH⊥y轴,垂足为点H,
![]() ,
,
![]() ,
,
![]() ,
,
∴ΔADC是等边三角形,
![]() ,
,![]() ,
,
![]()
![]() =
=![]() =
=![]() ,
,
∵S△OCD=![]() ,
,
![]() ;
;
(3)由(1)知,在Rt△OAB中,OA=3,OB=3![]() ,∠BAO=60°,AB=6,∠ABO=30°,
,∠BAO=60°,AB=6,∠ABO=30°,
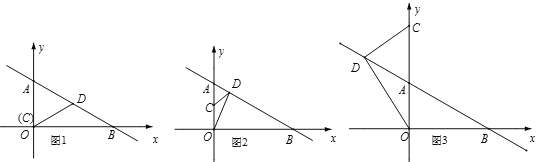
当△ODB为等腰三角形时,分三种情况进行讨论:
①如图1,当OD=DB时,D在OB的垂直平分线上,则D为AB的中点,AD=![]() AB=3,
AB=3,
∵CD=DA,∠CAD=60°,
∴△ACD是等边三角形,
∴AC=AD=3,
∴C与原点重合,
∴C点坐标为(0,0);
②如图2,当BD=BO=3![]() 时,AD=AB-BD=6-3
时,AD=AB-BD=6-3![]() ,
,
∵CD=DA,∠CAD=60°,
∴△ACD是等边三角形,
∴AC=AD=6-3![]() ,
,
∴OC=OA-AC=3-(6-3![]() )=3
)=3![]() -3,
-3,
∴C点坐标为(0,3![]() -3);
-3);
③如图3,当OD=OB=3![]() 时,∠ODB=∠OBD=30°,
时,∠ODB=∠OBD=30°,
∵∠AOD=∠BAO-∠ODB=60°-30°,
∴∠ODB=∠AOD=30°,
∴AD=OA=3,
∵CD=DA,∠CAD=60°,
∴△ACD是等边三角形,
∴AC=AD=3,
∴OC=OA+AC=3+3=6,
∴C点坐标为(0,6),
综上,点C的坐标为(0,0),![]() ,(0,6).
,(0,6).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩x(分) | 频数(人数) | 频率 |
一 | 50≤x<60 | 2 | 0.04 |
二 | 60≤x<70 | 10 | 0.2 |
三 | 70≤x<80 | 14 | b |
四 | 80≤x<90 | a | 0.32 |
五 | 90≤x<100 | 8 | 0.16 |
请根据表格提供的信息,解答以下问题:
(1)直接写出表中a= , b=;
(2)请补全右面相应的频数分布直方图;
(3)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .
(4)请根据得到的统计数据,简要分析这些同学的汉字书写能力,并为提高同学们的书写汉字能力提一条建议(所提建议不超过20字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形中,由三角形的内角平分线所形成的角存在一定的规律,理解并掌握其中的规律,有助于同学们巩固相关的数学知识.
如图1,![]() 中,
中,![]() 分别平分
分别平分![]() ,且相交于点
,且相交于点![]() “勤奋小组”的同学发现:
“勤奋小组”的同学发现:![]() .证明过程如下:
.证明过程如下:

证明:如图2,连接![]() 并延长,
并延长,

则![]() (依据1)
(依据1)
![]() 与
与![]() 分别平分
分别平分![]()
![]()
![]()
![]()
![]()
![]()
又![]() ,(依据2)
,(依据2)
![]() .
.
![]() 依据1是 ___,依据2是 __;
依据1是 ___,依据2是 __;
![]() 如图3,在图1的基础上,作
如图3,在图1的基础上,作![]() 的角平分线
的角平分线![]() 交于点
交于点![]() 试探究
试探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”
(1)请直接写出两个为“同簇二次函数”的函数:①______,②_________;
(2)已知关于![]() 的二次函数
的二次函数![]() 和
和![]() ,若
,若![]() 与
与![]() 为“同簇二次函数”,求函数
为“同簇二次函数”,求函数![]() 的表达式,并求出当
的表达式,并求出当![]() 时,
时,![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.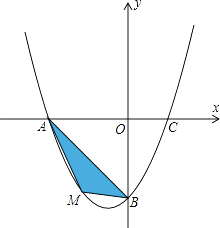
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.
求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=﹣x上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 上,点
上,点![]() ,
,![]() 在直线
在直线![]() 上,且
上,且![]() ,若
,若![]() 保持不动,线段
保持不动,线段![]() 向右匀速平移,如图2反映了
向右匀速平移,如图2反映了![]() 的长度
的长度![]() 随时间
随时间![]() 的变化而变化的情况,则:
的变化而变化的情况,则:



(1)在线段![]() 开始平移之前,
开始平移之前,![]()
![]() ;
;
(2)线段![]() 向右平移了
向右平移了 ![]() ,向右平移的速度是
,向右平移的速度是 ![]() ;
;
(3)如图3反映了![]() 的面积
的面积![]() 随时间
随时间![]() 的变化而变化的情况,则
的变化而变化的情况,则
①平行线![]() ,
,![]() 之间的距离是
之间的距离是 ![]() ;
;
②当![]() 时,直接写出
时,直接写出![]() 关于
关于![]() 的函数关系式(不必化简).
的函数关系式(不必化简).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自从新冠肺炎疫情爆发,我国高度重视并采取了强有力的措施进行防控,像钟南山爷爷和李兰娟奶奶等无数白衣天使为保卫大家的安全奋斗在抗疫一线. 武汉是疫情最先爆发的地区,“一方有难,八方支援”是中华传统美德,为了帮助武汉人民尽快度过难关,某校七年级全体同学参加了捐款活动.现随机抽查了部分同学捐款的情况统计如图所示:

(1)在本次调查中,一共抽查了_________名学生;
(2)请补全条形统计图,并计算在扇形统计图中,“捐款 20元”对应的圆心角度数是 度;
(3)在七年级600名学生中,捐款15元以上(不含15元)的学生估计有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com