
����Ŀ��һ���γ��Ӽ�ʻ���ҵأ������ҵغ��������ؼأ��ٶ���ԭ����1.5������������tСʱ.һ������ͬʱ�Ӽ�ʻ���ҵأ������ҵغ�ֹͣ.����ͬʱ������������ʻ����γ���ʻ��ʱ��Ϊx��h���������뿪�صľ���Ϊy��km����������ʻ������y��x֮��ĺ���ͼ����ͼ��ʾ.
��1���γ����ҵط��ؼص��ٶ�Ϊ km/t��t= h��
��2����γ����ҵط��ؼ�ʱy��x֮��ĺ�����ϵʽ��
��3�����γ��Ӽط����ҵص�;�����������ʱ�������������صľ���.
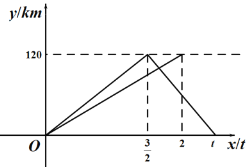
���𰸡�(1) 120��![]() ;(2) y=-120x+300; (3) 100km.
;(2) y=-120x+300; (3) 100km.
����������1������ͼ��ɵõ�x=![]() Сʱʱ����صľ�����120ǧ�ף�������ýγ��Ӽص��ҵص��ٶȣ�������ýγ����ҵط��ؼص��ٶȺ�t��ֵ��
Сʱʱ����صľ�����120ǧ�ף�������ýγ��Ӽص��ҵص��ٶȣ�������ýγ����ҵط��ؼص��ٶȺ�t��ֵ��
��2�����ô���ϵ����������⣻
��3�����ô���ϵ������ýγ����ҵص��صĺ�������ʽ�ͻ���·�̺�ʱ��ĺ�������ʽ�������꼴�ɣ�
��1��120��![]() .
.
��2����γ����ҵط��ؼصĺ�����ϵʽΪ��y=kx+b.
����![]() ��120���ͣ�
��120���ͣ�![]() ��0��������������룬��
��0��������������룬��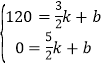 ��
��
��ã�![]() ��
��
���Խγ����ҵط��ؼ�ʱy��x֮��ĺ�����ϵʽΪ��y=-120x+300;
��3��������Ӽ�ʻ���ҵصĺ�����ϵʽΪ��y=ax ���㣨2,120�������ã����a=60���ʻ����Ӽ�ʻ���ҵ�ʱy��x֮��ĺ�����ϵʽΪ��y=60x.
��ͼ���֪���γ����ҵط��ؼ�ʱ������������·����ȣ���-120x+300=60x ���x=![]() ,��x=
,��x=![]() ʱ��y=100. �����������صľ���Ϊ100km
ʱ��y=100. �����������صľ���Ϊ100km



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��B��C������ֱ�Ϊ����1��0������5��0������0��2��������P��A���������x����������ÿ��1����λ���ȵ��ٶ���B���ƶ�������PC���ӳ�����E��ʹCE=PC�����߶�PE�Ƶ�P˳ʱ����ת90��õ��߶�PF������FB������P���ƶ��Ĺ����У�ʹ��PBF��Ϊֱ�������Σ����F�������� �� 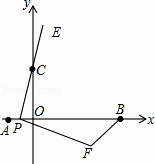
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ˮ��������������A�е�һ��ˮ�������������ۣ��л������������䷽ʽ����������е���ľ�Ϊ200Ԫ/ʱ��������Ҫ�ο��������£�
���乤�� | ;��ƽ���ٶ� (ǧ��/ʱ) | �˷� (Ԫ/ǧ��) | װж���� (Ԫ) |
�� | 100 | 15 | 2000 |
���� | 80 | 20 | 900 |
(1)���ѡ���������ܷ��ñ�ѡ����ܷ��ö�1100Ԫ����ô��֪��������A��֮���·���Ƕ���ǧ���������з��̽��
(2)��A����ij��֮���·��Ϊsǧ�ף���֪������������·�ϵ����ʱ��ֱ�Ϊ2Сʱ��3.1Сʱ��Ҫ�뽫����ˮ���������н������ۣ���sΪ����ʱ��ѡ��������������������ͬ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������Ϊ3��ֱ���ص���һ��ʹ��ABC=60�������ı���ABCD�������_____________
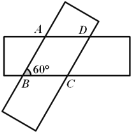
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̼�Ԥ��һ��Ӧ�������ܳ����г�������13200Ԫ������һ�����ֳ��������к��Ȼ����Ӧ���̼�����28800Ԫ�����˵ڶ������ֳ��������������ǵ�һ����������2���������۹���10Ԫ��
��1�����̼ҹ����ĵ�һ�������Ƕ��ټ���
��2����������������ͬ�ı�����ۣ����ʣ��50���������Ż������������������ȫ�������������25%���������������أ�����ôÿ�������ı�������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�A��ʾ����Ϊ6��B����������A����һ�㣬��A��B�����ľ���Ϊ10������P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
��1����B��ʾ������_____��
��2������Q�ӵ�B��������ÿ��4����λ���ȵ��ٶ����������������˶�������P��Qͬʱ����������P�˶�_____��ʱ����P���Q��ľ���Ϊ8����λ���ȣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�������ڽ�����ı��ν����Ƚ��ı��Σ�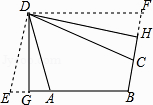
��1�����Ƚ��ı���ABCD�У���A=��B=��C�����A��ȡֵ��Χ��
��2����ͼ���۵�ƽ���ı���ֽƬDEBF��ʹ����E��F�ֱ����ڱ�BE��BF�ϵĵ�A��C�����ۺ۷ֱ�ΪDG��DH����֤���ı���ABCD�����Ƚ��ı��Σ�
��3�����Ƚ��ı���ABCD�У���A=��B=��C��90�㣬��CB=CD=4����AD�ij�Ϊ��ֵʱ��AB�ij���������ֵ�Ƕ��٣�����ͼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֿ������ʳ60![]() ������������⣬3��С�ⶼҪд����Ҫ�Ľ�����̣�
������������⣬3��С�ⶼҪд����Ҫ�Ľ�����̣�
��1���ײֿ��˽���ʳ14![]() ���Ҳֿ��˳���ʳ10
���Ҳֿ��˳���ʳ10![]() �������ֿ����ʳ������ȣ��ס��������ֿ�ԭ�����ж�����ʳ��
�������ֿ����ʳ������ȣ��ס��������ֿ�ԭ�����ж�����ʳ��
��2������ײֿ�ԭ�е���ʳ���Ҳֿ��2����3![]() ����ײֿ��˳�����
����ײֿ��˳�����![]() ��ʳ���Ҳֿ⣬��ʹ�ס������ֿ���ʳ������ȣ�
��ʳ���Ҳֿ⣬��ʹ�ס������ֿ���ʳ������ȣ�
��3���������ֿ�ͬʱ�˽���ʳ���ײֿ��˽��������ȱ��ֿ�ԭ����ʳ������һ���1![]() ���Ҳֿ��˽��������DZ��ֿ�ԭ����ʳ��������8
���Ҳֿ��˽��������DZ��ֿ�ԭ����ʳ��������8![]() ���õĺ͵�һ�������ʱ�ס������ֿ����ʳ����
���õĺ͵�һ�������ʱ�ס������ֿ����ʳ����![]() ?
?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�CE��AB��AB�ӳ����ڵ�E����FΪ��B����CE�ĶԳƵ㣬����CF���ֱ��ӳ�DC��CF����G��H��ʹFH=CG������AG��DH���ڵ�P��
��1�������ⲹȫͼ1��
��2������AG��DH��������ϵ��֤����
��3������DAB=70�����Ƿ���ڵ�G��ʹ����ADPΪ�ȱ������Σ������ڣ����CG�ij����������ڣ�˵�����ɣ�


�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com