
【题目】如图,已知BE和CF是△ABC的两条高,∠ABC=48°,∠ACB=76°,则∠FDE= . 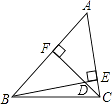
【答案】124°
【解析】解:(法一)在△ABC中, ∵∠A+∠ABC+∠ACB=180°
∴∠A=180°﹣48°﹣76°=56°
在四边形AFDE中,
∵∠A+∠AFC+∠AEB+∠FDE=360°
又∵∠AFC=∠AEB=90°,∠A=56°
∴∠FDE=360°﹣90°﹣90°﹣56°
=124°
故答案为:124°
(法二)∵∠AEB=∠ACB+∠EBC=90°,∠AFC=∠ABC+∠FCB=90°,
∴∠CBE=14°,∠FCB=42°,
∵∠BDC=180°﹣∠CBE﹣∠FCB=124°,
∴∠FDE=124°.
故答案为:124°
由三角形的内角和定理求出∠A的度数,再有四边形AFDE的内角和求出∠FDE的度数.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=30°.
(1)如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC=°. 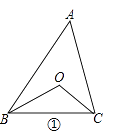
(2)如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2 , 则∠BO2C=°. 
(3)如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示). 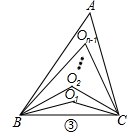
(4)如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1 , 若∠BOn﹣1C=60°,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1>x2,与y轴交于点C(0,4),其中x1、x2是方程x2-2x-8=0的两个根.
(1)求这条抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PE∥AC,交BC于点E,连接CP,当△CPE的面积最大时,求点P的坐标;
(3)探究:若点Q是抛物线对称轴上的点,是否存在这样的点Q,使△QBC成为等腰三角形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.
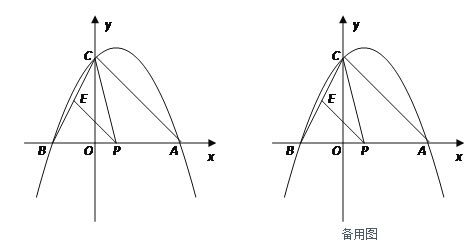
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据国家统计局数据,2018年全年国内生产总值为90.3万亿,比2017年增长6.6%.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破100万亿的年份是( )
A. 2019年B. 2020年C. 2021年D. 2022年
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第十六届海峡交易会对接合同项目2049项,总投资682亿元.将682亿用科学记数法表示为( )
A. 0.682×1011B. 6.82×1010C. 6.82×109D. 682×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
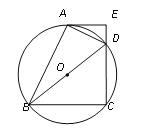
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明“三角形的外角和等于360°”. 如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.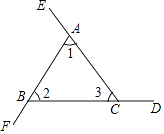
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com