
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t秒.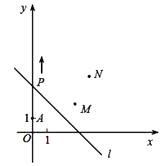
(1)当t=3时,求l的解析式;
(2)若点M , N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
【答案】
(1)解:直线 ![]() 交y轴于点P(0,b),由题意得 ,b>0, t≥0 , b=1+t ,
交y轴于点P(0,b),由题意得 ,b>0, t≥0 , b=1+t ,
当t=3时,b=4 ∴ ![]()
(2)解:当直线 ![]() 过M(3,2)时,
过M(3,2)时, ![]() 解得b=5
解得b=5
5=1+t
∴t=4
当直线 ![]() 过N(4,4)时
过N(4,4)时
![]() 解得 b=8,8=1+t ∴t=7 ∴ M,N位于l的异侧时,t的取值范围是 :4<t<7 。
解得 b=8,8=1+t ∴t=7 ∴ M,N位于l的异侧时,t的取值范围是 :4<t<7 。
(3)解:如图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E. F为点M在坐标轴上的对称点。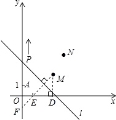
过点M作MD⊥x轴于点D,则OD=3,MD=2.
根据对称性知:∠MED=∠OEF=45,则△MDE与△OEF均为等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,1).
∵M(3,2),F(0,1),
∴线段MF中点坐标为(![]() ,
,![]() ).
).
直线y=x+b过点(![]() ,
,![]() ),则
),则![]() =
=![]() +b,解得:b=2,
+b,解得:b=2,
2=1+t,
解得t=1.
∵M(3,2),E(1,0),
∴线段ME中点坐标为(2,1).
直线y=x+b过点(2,1),则1=2+b,解得:b=3,
3=1+t,
解得t=2.
故点M关于l的对称点,当t=1时,落在y轴上,当t=2时,落在x轴上 。
【解析】(1)利用一次函数图象上点的坐标特征,求出一次函数的解析式;
(2)分别求出直线l经过点M、点N时的t值,即可得到t的取值范围;
(3)找出点M关于直线l在坐标轴上的对称点E、F,如解答图所示.求出点E、F的坐标,然后分别求出ME、MF中点坐标,最后分别求出时间t的值.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
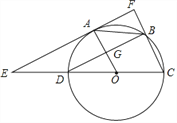
【题目】如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形。过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.
(1)求证:EF是⊙O的切线;
(2)求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列五个命题:
①如果两个数的绝对值相等,那么这两个数的平方相等;
②内错角相等;
③在同一平面内,垂直于同一条直线的两条直线互相平行;
④两个无理数的和一定是无理数;
⑤坐标平面内的点与有序数对是一一对应的.
其中真命题的个数是( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年10月1日,重庆四大景区共接待游客约518 000人,这个数可用科学记数法表示为( )
A.0.518×104
B.5.18×105
C.51.8×106
D.518×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择.如果调整文具的购买品种,每减少购买1个甲种文具,需增加购买2个乙种文具.设购买x个甲种文具时,需购买y个乙种文具.
(1)①当减少购买1个甲种文具时,x= ,y= ;②求y与x之间的函数表达式.
(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元.甲、乙两种文具各购买了多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com